Question

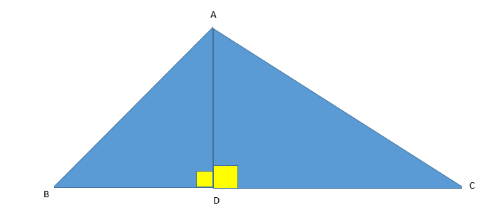
In $\vartriangle ABC,\angle A = {90^ \circ }$. If AD is perpendicular to BC, then prove that $\vartriangle BDA \sim \vartriangle ADC$.

Answer 1

Hint: We will consider both the triangles $\vartriangle BDA$ and $\vartriangle ADC$. Now using the right angles in both of them and the fact that $\angle A = {90^ \circ }$, we will prove one more of the corresponding angle to be equal. Then, by using the AA- similarity criterion, we will have the required proof.

Complete step-by-step answer:
Let us first consider $\angle A = {90^ \circ }$.
$\angle BAD + \angle DAC = {90^ \circ }$ (Each $\angle A = {90^ \circ }$ given in the question only) ………(1)
Now, consider $\vartriangle ADC$, we will have:-
$\angle CDA + \angle DCA + \angle DAC = {180^ \circ }$ ……….(2)
Since we already have $\angle CDA = {90^ \circ }$ and using (1) in (2), we will get:-
$ \Rightarrow {90^ \circ } + \angle DCA + {90^ \circ } - \angle BAD = {180^ \circ }$
$ \Rightarrow \angle DCA - \angle BAD = 0$
$ \Rightarrow \angle DCA = \angle BAD$ ……..(3)
Consider the $\vartriangle BDA$ and $\vartriangle ADC$ :
$\angle ADB = \angle CDA$ (Each ${90^ \circ }$ given in the question only)
$\angle DCA = \angle BAD$ (Using (3))
Hence, $\vartriangle BDA \cong \vartriangle ADC$ (By AA similarity criterion)
[If two triangles are similar it means that all corresponding angle pairs are congruent and all corresponding sides are proportional. The AA criterion for triangle similarity states that if two triangles have two pairs of congruent angles, then the triangles are similar]
Hence, proved.

Note: The students must note how the AA similarity criterion works. Let us discuss it now.
We know that by Angle sum property, we will have the sum of all interior angles to be equal to ${180^ \circ }$. So, if two of the angles are already equal, therefore, the third must be the difference of ${180^ \circ }$ and the sum of both other angles. Ideally, the name of this criterion should then be the AAA (Angle-Angle-Angle) criterion, but we call it as AA criterion because we need only two pairs of angles to be equal - the third pair will then automatically be equal by angle sum property of triangles.
The students must know the difference between similar triangles and the congruent triangles. The difference is as follows:
When figures have the same shape but may be different in size, they are called similar figures.
Figures that are the same size and the same shape are congruent figures.