Question

In \[\vartriangle ABC\], the median AD divides \[\angle BAC\]such that \[\angle BAD:\angle CAD = 2:1\]. Then \[\cos \left( {\dfrac{A}{3}} \right)\] is equal to
A.\[\dfrac{{\sin B}}{{2\sin C}}\]
B. \[\dfrac{{\sin C}}{{2\sin B}}\]
C. \[\dfrac{{2\sin B}}{{\sin C}}\]
D. None of these

Answer 1

Hint: Use the given ratio of angles to write the measure of the angle in terms of angle A. We use the law of sines to write the ratio of side and sine of the opposite angle. Find the length AD from applying the law of sine in both triangles made by the median AD. Equate both the lengths obtained.
* Law of sine states that in a triangle ABC the ratio of side of a triangle to the sine of opposite angle is same for all the sides of the triangle, i.e. if side a has opposite angle A, side b has opposite angle B and side c has opposite angle C, then we can write \[\dfrac{{\sin A}}{a} = \dfrac{{\sin B}}{b} = \dfrac{{\sin C}}{c} = k\] where k is some constant term.
* Median is a line that joins a vertex and midpoint of the opposite side.

Complete step by step solution:
We draw a triangle ABC having vertices A, B and C having sides opposite to each angle as a, b and c respectively. Median AD divides side BC in two halves.

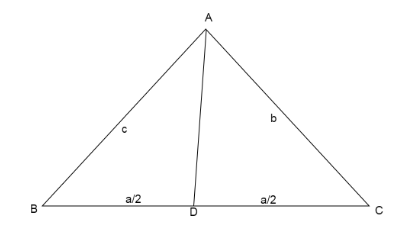
We are given that the median AD divides \[\angle BAC\] such that \[\angle BAD:\angle CAD = 2:1\]
Use the concept of ratio to write the angles in fractional form
\[ \Rightarrow \dfrac{{\angle BAD}}{{\angle CAD}} = \dfrac{2}{1}\]
Cross multiply the terms
\[ \Rightarrow \angle BAD = 2\angle CAD\]...................… (1)
Since we know \[\angle BAC = \angle BAD + \angle CAD\]
Substitute the values in equation (1)
\[ \Rightarrow \angle BAC = 2\angle CAD + \angle CAD\]
\[ \Rightarrow \angle BAC = 3\angle CAD\]
We write \[\angle BAC = A\]
\[ \Rightarrow A = 3\angle CAD\]
Divide both sides by 3
\[ \Rightarrow \dfrac{A}{3} = \angle CAD\]..................… (2)
Substitute value from equation (2) in (1)
 \[ \Rightarrow \angle BAD = \dfrac{{2A}}{3}\]..................… (3)
Now we apply the law of sine in both triangles made by the median separately.
In \[\vartriangle BAD\]
\[\dfrac{{BD}}{{\sin (\angle BAD)}} = \dfrac{{AD}}{{\sin B}}\]
Substitute the value of BD and angle BAD from equation (3)
\[ \Rightarrow \dfrac{{a/2}}{{\sin (\dfrac{{2A}}{3})}} = \dfrac{{AD}}{{\sin B}}\]
Shift all values except AD to one side of the equation
\[ \Rightarrow \dfrac{{(a/2)\sin B}}{{\sin (\dfrac{{2A}}{3})}} = AD\].................… (4)
In \[\vartriangle CAD\]
\[\dfrac{{CD}}{{\sin (\angle CAD)}} = \dfrac{{AD}}{{\sin C}}\]
Substitute the value of CD and angle CAD from equation (2)
\[ \Rightarrow \dfrac{{a/2}}{{\sin (\dfrac{A}{3})}} = \dfrac{{AD}}{{\sin C}}\]
Shift all values except AD to one side of the equation
\[ \Rightarrow \dfrac{{(a/2)\sin C}}{{\sin (\dfrac{A}{3})}} = AD\]....................… (5)
Since AD is the median and will have fixed length, we equate values from (4) and (5)
\[ \Rightarrow \dfrac{{(a/2)\sin B}}{{\sin (\dfrac{{2A}}{3})}} = \dfrac{{(a/2)\sin C}}{{\sin (\dfrac{A}{3})}}\]
Cancel same terms from both sides of the equation
\[ \Rightarrow \dfrac{{\sin B}}{{\sin (\dfrac{{2A}}{3})}} = \dfrac{{\sin C}}{{\sin (\dfrac{A}{3})}}\]
Since we know trigonometric identity \[\sin 2x = 2\sin x\cos x\]
\[ \Rightarrow \dfrac{{\sin B}}{{2\sin (\dfrac{A}{3})\cos (\dfrac{A}{3})}} = \dfrac{{\sin C}}{{\sin (\dfrac{A}{3})}}\]
Cancel same terms from both sides of the equation
\[ \Rightarrow \dfrac{{\sin B}}{{2\cos (\dfrac{A}{3})}} = \dfrac{{\sin C}}{1}\]
Cross multiply values from both sides
\[ \Rightarrow \dfrac{{\sin B}}{{2\sin C}} = \cos (\dfrac{A}{3})\]
\[\therefore \]The value of \[\cos \left( {\dfrac{A}{3}} \right)\] is equal to \[\dfrac{{\sin B}}{{2\sin C}}\].

\[\therefore \]Option A is correct.

Note: Students are likely to make mistakes when applying sine law as they tend to write wrong sides opposite to the respective angle, keep in mind we write the side opposite to the angle as the side that does not touch the angle at all.
Also, while cross multiplying always brings the value of numerator to denominator and vice versa. Students get confused while writing the sine formula, keep in mind we take the opposite side to the angle in numerator and the sine of the angle in the denominator. Also, many books state that sine rule can be written as \[\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = k\] which is one and the same thing.