Question

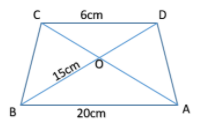
In trapezium ABCD, side AB is parallel to side DC and diagonals AC and BD intersect each other in point O. If AB = 20. DC = 6, OB = 15. Then find the length of OD.

Answer 1

Hint: Now we know that the AB is parallel to CD hence we have alternate angles that are equal. Also we know that opposite angles are equal if intersection points are equal. Hence using these conditions in triangle DOC and triangle BOA we can prove the triangles are similar by AAA test. Hence by CPCT we can find the length of OD.

Complete step-by-step answer:
Now we are given that ABCD is a trapezium with AB parallel to DC and AC and BD intersect each other at point O. Hence we obtain two triangles, triangle DOC and triangle BOD.
Now first let us consider the two parallel lines AB and CD. Now we know that alternate angles in parallel lines are equal. Hence we have
$\angle ODC=\angle OBA............(1)$
And also we have
$\angle OAB=\angle OCD..............(2)$
Now we have that AC and BD intersect at O
And we know that opposite angles are equal at intersection point hence we get
$\angle COD=\angle AOB..................(3)$
Now consider triangle AOB and triangle COD
From equation (1), equation (2) and equation (3) we get.
$\angle ODC=\angle OBA$
$\angle OAB=\angle OCD$
$\angle COD=\angle AOB$
Hence by AAA test of similarity we get that the triangles are similar.
Hence we get $\Delta COD\sim \Delta AOB$
Now we know that in similar triangle corresponding sides are in proportion, hence we get
$\dfrac{CD}{OD}=\dfrac{AB}{OB}$
Hence substituting the values we get.
$\dfrac{6}{OD}=\dfrac{20}{15}$
Now cross multiplying we get
6 × 15 = 20 × OD
Hence, 90 = 20 × OD
Dividing the equation by 20 we get
OD = 4.5
Hence the length of OD is 4.5cm.

Note: Now note that while writing the triangles as similar triangles the sides and angles should be in proper order. For example if we have $\Delta COD\sim \Delta AOB$ it cannot be written as $\Delta COD\sim \Delta BOA$ .