Question

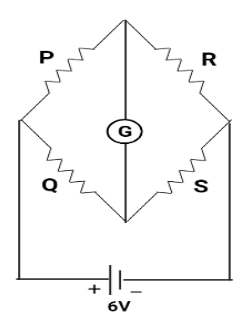
In the wheatstone’s network given, $P = 10\Omega ,Q = 20\Omega ,R = 15\Omega ,S = 30\Omega ,$ the current passing through the battery (of negligible internal resistance) is:
A. $0.36A$
B. $Zero$
C. $0.18A$
D0 $0.72A$

Answer 1

Hint:The Wheatstone bridge operates on the null deflection theorem, which states that their resistance ratios are identical and that no current passes through the circuit. In normal circumstances, the bridge is unbalanced, allowing current to pass through the galvanometer.

Complete step by step answer:
In the question it is given that,
$P = 10\Omega \\
\Rightarrow Q = 20\Omega \\
\Rightarrow R = 15\Omega \\
\Rightarrow S = 30\Omega \\ $
Now , we see that
$\dfrac{P}{Q} = \dfrac{{10}}{{20}} = \dfrac{1}{2}$
Similarly,
$\dfrac{R}{S} = \dfrac{{15}}{{30}} = \dfrac{1}{2}$
From the above two equations, We observe that $\dfrac{P}{Q} = \dfrac{R}{S}$ which states that their resistance ratios are identical. Hence, there is no current flowing through the galvanometer. Therefore, The Wheatstone bridge is satisfied.
Now, we see that $P$ and $R$ are in series. Hence, the net resistance will be,
${R_1} = P + R \\
\Rightarrow {R_1} = 10\Omega + 15\Omega \\
\Rightarrow {R_1} = 25\Omega \\ $
Similarly, $Q$ and $S$ are also in series. Hence, the net resistance will be,
${R_2} = Q + S \\
\Rightarrow {R_2} = 20\Omega + 30\Omega \\
\Rightarrow {R_2} = 50\Omega \\$
Now, ${R_1}$ and ${R_2}$ are in parallel combination,
$\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
$\Rightarrow \dfrac{1}{R} = \dfrac{1}{{50}} + \dfrac{1}{{25}} \\
\Rightarrow \dfrac{1}{R} = \dfrac{{1 + 2}}{{50}} \\
\Rightarrow \dfrac{1}{R} = \dfrac{3}{{50}} \\
\Rightarrow R = \dfrac{{50}}{3} \\ $
Using ohm’s law, $I = \dfrac{V}{R}$
We know that,
$V = 6V \\
\Rightarrow R = \dfrac{{50}}{3}\Omega \\ $
Substituting these values we get,
$I = \dfrac{V}{R} \\
\Rightarrow I = \dfrac{{6 \times 3}}{{50}} \\
\Rightarrow I = \dfrac{{18}}{{50}} \\
\therefore I = 0.36A \\ $
Hence, the correct answer is option A.

Note:A Wheatstone bridge is an electrical circuit that balances two legs of a bridge circuit, one of which contains the unknown part, to test an unknown electrical resistance. The circuit's main advantage is its ability to produce highly precise measurements.