Question

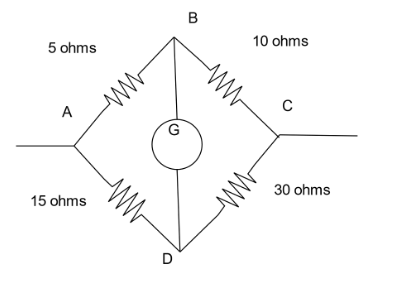
In the Wheatstone's bridge shown it current \[2A\] enters at A, then what is the value of current in arm BC?

Answer 1

Hint: A Wheatstone bridge is an electrical circuit used to measure an unknown electrical resistance by adjusting two legs of an extension circuit, one leg of which incorporates the unknown segment. The essential advantage of the circuit is its capability to give amazingly accurate estimations

Formula used:
\[\dfrac{P}{Q} = \dfrac{R}{S}\]
Where, $P, Q, R$ and $S$ are electrical resistances.
Ohm’s law: \[V = IR\]

Complete step by step answer:
It is given that a current of \[2A\] is passing through the vertex A. Let the current flowing through the arm ABC be \[I\,Amperes\].The current flowing through the arm ADC will be the remaining left from the value of \[2A\].The current flowing through the arm ADC be \[\left( {2 - I} \right)\,Amperes\].Since the voltage flowing through the circuit is unknown, we can take it as \[V\].

The net resistance in arm ABC will be \[{R_{ABC}} = 10 + 5 = 15\]
The net resistance in arm ADC will be \[{R_{ADC}} = 30 + 15 = 45\]
We know that ohm’s law gives us the relation between current, resistance and voltage.
\[V = 15I\]
\[\Rightarrow V = 45(2 - I) = 90 - 45I\]
The voltage through arms ABC and ADC are the same, so we arrive at the equation:
Equating these two equations against each other, we have
\[15I = 90 - 45I \\
\Rightarrow (45 + 15)I = 90 \]
In order to find the value of current flowing through arm ABC, we have to isolate the variables and the constants, that gives us:
\[\therefore I = \dfrac{{90}}{{60}} = 1.5A\]

Therefore, the current flowing through arm ABC is \[1.5\,A\].

Note: In wheatstone bridge, under balanced conditions no current flows from the galvanometer. The galvanometer is a device that detects the presence of current. It also measures the very low or feeble current flowing through the circuit. The essential advantage of the circuit is its capability to give amazingly accurate estimations.