Question

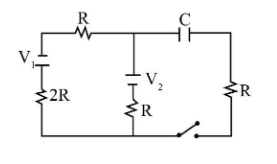
In the transient current circuit shown, the time constant is:

(1) \[\dfrac{5}{3}RC\]
(2) \[\dfrac{5}{2}RC\]
(3) \[\dfrac{7}{4}RC\]
(4) \[\dfrac{7}{3}RC\]

Answer 1

Hint: We will use the concept of Thevenin’s theorem to reduce the given network into its simplest form. We will also use the expressions for equivalent resistance when two resistors are in parallel or series combinations. Also, the time constant of the given circuit is equal to the product of capacitance and equivalent resistance of the given circuit.

Complete step by step answer:
According to the concept of Thevenin’s theorem, we can replace several voltages by a single power supply and several resistances by one single resistance, which is connected in series with the load.
We can write the expression for equivalent resistance by analyzing the circuit from the right-hand side, short circuit all the voltages, and opening the resistance R at extreme right.
The equivalent of two resistors connected in series is given by:
\[{R_s} = {R_1} + {R_2}\]…….(1)
The resistors of resistances R and 2R are connected in series, therefore substituting R for \[{R_1}\]and 2R for \[{R_2}\]the above expression.
\[\begin{array}{l}
{R_s} = R + 2R\\
= 3R
\end{array}\]
We know that the equivalent resistance of two resistors connected in parallel is given by:
\[{R_p} = \dfrac{{{R_3}{R_4}}}{{{R_3} + {R_4}}}\]
We can see that the resistor of equivalent resistance 3R and R are in parallel. Therefore we will substitute R for \[{R_3}\] and 2R for \[{R_4}\] in the above expression.
\[\begin{array}{l}
{R_p} = \dfrac{{\left( R \right)\left( {3R} \right)}}{{R + 3R}}\\
= \dfrac{3}{4}R
\end{array}\]
The equivalent resistance of the circuit can be obtained by substituting the series combination of resistance \[\dfrac{3}{4}R\] for \[{R_1}\] and R for \[{R_2}\].
\[\begin{array}{l}
{R_{eq}} = \dfrac{3}{4}R + R\\
= \dfrac{7}{4}R
\end{array}\]
We know that the time constant is given by the product of equivalent resistance and capacitance of the circuit.
\[\tau = {R_{eq}}C\]
On substituting \[\dfrac{7}{4}R\] for \[{R_{eq}}\] in the above expression, we get:
\[\begin{array}{l}
\tau = \left( {\dfrac{7}{4}R} \right)C\\
= \dfrac{7}{4}RC
\end{array}\]
Therefore, the time constant of the given circuit is \[\dfrac{7}{4}RC\], and option (3) is correct.

Note: Do not take the extreme right resistance of the circuit into consideration while converting the given circuit into its reduced form using Thevenin’s theorem. This has to be open and will be treated as a load.