Question

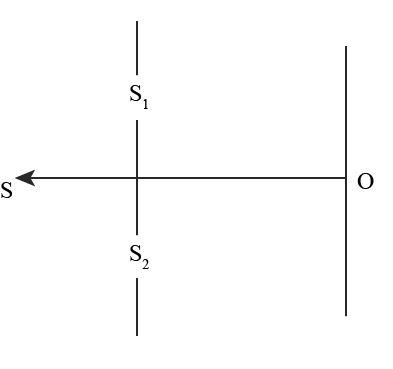
In the set up shown, the two slits ${S_1}$ and ${S_2}$ are not equidistant from the slit. The central fringe at $O$ is then

(A) always bright
(B) always dark
(C) either dark or bright depending on the position of S
(D) neither dark nor bright

Answer 1

Hint: This question uses the concept of Young’s Double Slit experiments. You need to apply the formula for the path difference for both dark fringe and bright fringe. On comparing both the obtained expression, you can figure out the correct answer.

Complete step by step answer:
As we know that the expression for the path difference can be given as,
$\Delta d = \left( {S{S_1} + {S_1}O} \right) - \left( {S{S_2} + {S_2}O} \right)$

In the case for the maximum intensity, the above expression would be equal to $n\lambda $. It means, this can be written as,
$\left( {S{S_1} + {S_1}O} \right) - \left( {S{S_2} + {S_2}O} \right) = n\lambda $
Here, the value of n varies as $1,\;2,\;3,\;4,.........$.

Similarly for the minimum intensity, the expression would be equal to $\left( {n - \dfrac{1}{2}} \right)\lambda $. It means, this can be written as,
$\left( {S{S_1} + {S_1}O} \right) - \left( {S{S_2} + {S_2}O} \right) = \left( {n - \dfrac{1}{2}} \right)\lambda $
Here, the value of n varies as $1,\;2,\;3,\;4,.........$.

As both the slits ${S_1}$ and ${S_2}$ are not equidistant from the slit S. So the distance traveled by the light through ${S_1}$ and ${S_2}$ may not differ by integral multiple of the value of wavelength.
So, when the path difference $\Delta d$ will be equal to the $n\lambda $, the fringe will be bright.

Similarly in the other case, when the path difference $\Delta d$ will be equal to the $\left( {n - \dfrac{1}{2}} \right)\lambda $, the fringe will be dark.

Therefore, the fringe may be dark or bright depending upon the position of S.

Thus, option (C) is correct.

Note:
You may go wrong while comparing both the expression for the bright fringe and dark fringe. The bright and dark fringes are obtained due to overlapping of the light waves that are originated by two slits and the central fringe depends on the position of slits from the source.