Question

In the pulley system shown in the given figure, the movable pulleys A, B and C are of mass 1kg each, D and E are fixed pulleys. The strings are light and inextensible. Choose the correct alternative(s). All pulleys are frictionless.
                      

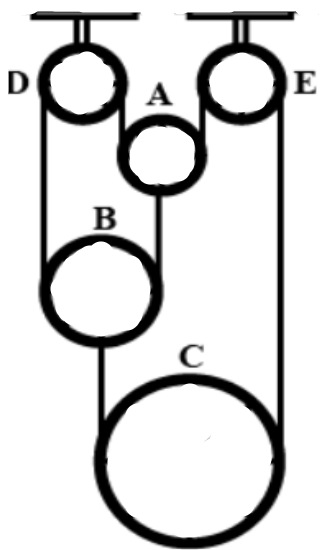
A) Tension in the string is \[\dfrac{20}{3}N\].
B) Acceleration of pulley A is \[\dfrac{g}{3}\]downward.
C) Acceleration of pulley B is \[\dfrac{g}{6}\]upward.
D) Acceleration of pulley C is \[\dfrac{g}{3}\]upward.

Answer 1

Hint: We need to find the tension acting on each of the strings attached to the pulleys to find the relation existing between them. The rigid pulleys cannot change their position, whereas the movable pulleys are moved according to the force on them.

Complete answer:
We know that the tension on all the wires is the same ‘T’ as they are connected throughout.
                               

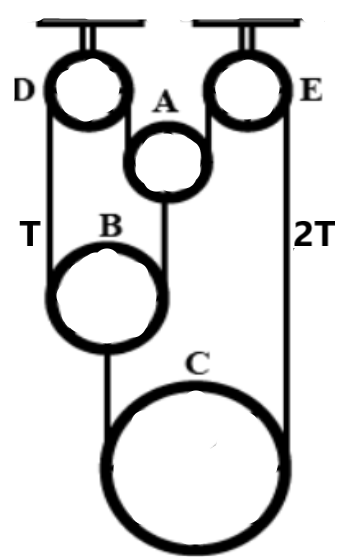
We can consider the acceleration on each of the pulley A, B, and C as \[{{\text{a}}_{\text{A}}}\text{, }{{\text{a}}_{\text{B}}}\text{ and }{{\text{a}}_{\text{c}}}\]all acting downward. We can equate the tension on the pulleys as –
\[\begin{align}
  & T{{a}_{A}}+T{{a}_{B}}+2T{{a}_{C}}=0 \\
 & \Rightarrow {{a}_{A}}+{{a}_{B}}+2{{a}_{C}}=0\text{ --(1)} \\
\end{align}\]
We know that according to Newton's second law of motion, the weight is proportional to the acceleration. We can substitute this in the given situation for all the movable pulleys. The difference in their weights and the tension acting on them gives the net force acting on them as –
\[\begin{align}
  & mg-T=ma \\
 & \Rightarrow \text{ }mg-T=m{{a}_{A}}\text{ --(a)} \\
 & \Rightarrow \text{ }mg-T=m{{a}_{B}}\text{ --(b)} \\
 & \Rightarrow \text{ }mg-2T=m{{a}_{C}}\text{ --(c)} \\
\end{align}\]
We can substitute this in case of each of the pulleys A, B and C as –
\[\begin{align}
  & 1(10)-T=1({{a}_{A}}) \\
 & \Rightarrow \text{ }10-T={{a}_{A}}\text{ --(2)} \\
 & 1(10)-T=1({{a}_{B}}) \\
 & \Rightarrow \text{ }10-T={{a}_{B}}\text{ --(3)} \\
 & 1(10)-2T=1({{a}_{C}}) \\
 & \Rightarrow \text{ }10-2T={{a}_{C}}\text{ --(4)} \\
\end{align}\]
Now, we can substitute these to get the acceleration of each pulley.
From (2) and (4), we get,
\[{{a}_{A}}-{{a}_{C}}=T\]
We can substitute this in (2),
\[\begin{align}
  & 10-{{a}_{A}}-{{a}_{C}}={{a}_{A}} \\
 & \Rightarrow \text{ 2}{{a}_{A}}+{{a}_{C}}=10\text{ --(5)} \\
\end{align}\]
Now, we can solve (2) and (4) as –
\[\begin{align}
  & {{a}_{A}}={{a}_{B}}=\dfrac{10}{3} \\
 & \text{and,} \\
 & {{a}_{C}}=\dfrac{-10}{3} \\
\end{align}\]
Now, we can calculate the tension T as –
\[T={{a}_{A}}-{{a}_{C}}=\dfrac{10}{3}-\dfrac{-10}{3}=\dfrac{20}{3}N\]
The tension on the wire of the pulley at some point is \[T=\dfrac{20}{3}N\].
Now, from (a), (b) and (c) we can derive that –
\[{{a}_{A}}+{{a}_{B}}={{a}_{C}}+g\]
But from (1),
\[{{a}_{A}}+{{a}_{B}}=-2{{a}_{C}}\]
i.e.,
\[{{a}_{C}}=\dfrac{g}{3}\]
Also, we can derive that –
\[{{a}_{A}}={{a}_{B}}=-\dfrac{g}{3}\]
We get that the acceleration of A and B is upward whereas, for C it is downwards.

The correct answer is/are options A, B and D.

Note:
The final equation seems to have a unit error as the accelerations add to give the tension. But the equation is right, it is because in this case the mass is unity and therefore it is coming up with the equation, but is present in the unit of the left-hand side.