Question

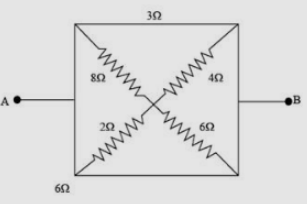
In the network shown, the equivalent resistance between A and B is

A. \[\dfrac{4}{3}\;\Omega \]
B. \[\dfrac{3}{4}\;\Omega \]
C. \[\dfrac{{24}}{{17}}\;\Omega \]
D. \[\dfrac{{17}}{{24}}\;\Omega \]

Answer 1

Hint:The above problem can be resolved using the concept and the fundamentals of the network analysis. The network diagrams consist of various resistances, connected in series as well as in parallel connection. These arrangements are resolved by undertaking the mathematical formulas for the series arrangement as well as the parallel arrangements. Moreover, these concepts are critical in resolving the phenomenal analysis of voltage drop and the current flow through the circuit.

Complete step by step answer:
From the given network diagram, the resistance \[8\;\Omega \] and \[2\;\Omega \] from point A are in parallel combination. Then, the net resistance is,
\[
\dfrac{1}{{{R_1}}} = \dfrac{1}{{8\;\Omega }} + \dfrac{1}{{2\;\Omega }}\\
\Rightarrow{R_1} = \dfrac{8}{5}\;\Omega
\]
Now from point B, the resistance \[4\;\Omega \] and \[6\;\Omega \] are also in parallel combination. Then the net resistance is,
\[
\dfrac{1}{{{R_2}}} = \dfrac{1}{{4\;\Omega }} + \dfrac{1}{{6\;\Omega }}\\
\Rightarrow{R_2} = \dfrac{{12}}{5}\;\Omega
\]
Now, as we can see that the above net resistances \[{R_1}\] and \[{R_2}\] are in series. Therefore, they contribute a resistance of magnitude,
\[
{R_s} = {R_1} + {R_2}\\
\Rightarrow{R_s} = \dfrac{8}{5}\;\Omega + \dfrac{{12}}{5}\;\Omega \\
\Rightarrow{R_s} = 4\;\Omega
\]
Clearly, the above resistances are parallel to the resistors of \[3\;\Omega \] and \[6\;\Omega \].
Then, the resistance across the terminals AB is given as,
\[
\dfrac{1}{{{R_{AB}}}} = \dfrac{1}{{4\;\Omega }} + \dfrac{1}{{3\;\Omega }} + \dfrac{1}{{6\;\Omega }}\\
\therefore{R_{AB}} = \dfrac{4}{3}\;\Omega
\]
 Therefore, the equivalent resistance between A and B is \[\dfrac{4}{3}\;\Omega \] and option (A) is correct.

Note: To resolve the given problem, one must understand the key concept behind the network analysis and some derived mathematical relations. These relations are obtained once we easily predict the phenomenal variation of current and the voltage along each of such paths in an electronic circuit. It is observed that the net resistance for the circuit is always coming out to be more as compared to the net resistance in the parallel connection.