Question

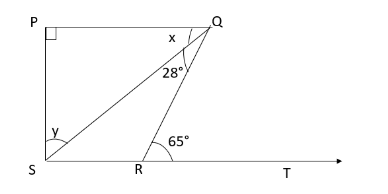
In the given figure, if $ PQ \bot PS,PQ\parallel SR,\angle SQR = 28^\circ and\angle QRT = 65^\circ , $ then find the values of $ x $ and $ y. $

Answer 1

Hint: The sum of all angles of a triangle is $ 180^\circ . $ Use this to find a relation between $ x $ and $ y $ . Then use the property that a straight line SRT will have angle $ {180^0} $ , to find the value of $ y $ . Which will in turn will help to find the value of $ x $ .

Complete step-by-step answer:
Since, a straight line makes an angle of $ {180^0} $ . We can write
 $ \angle QRS + \angle QRT = 180^\circ $
 $ \Rightarrow \angle QRS + 65^\circ = 180^\circ $
By simplifying it, we get
 $ \angle QRS = 115^\circ $ . . . . (1)
Now, In $ \Delta QRS $
Since, the sum of the angles of a triangle is $ {180^0} $ . We can write
 $ \angle QRS + \angle QSR + \angle RQS = 180^\circ $
By using equation (1), we can simplify above equation as
 $ \Rightarrow {115^0} + \angle QSR + 28^\circ = 180^\circ $
By simplifying it, we get
 $ \angle QSR = 37^\circ $ . . . . (2)
Now, since, $ PQ \bot PS $ , we can also say that, $ ST \bot PS $
Thus, $ \angle PSR = {90^0} $
Therefore, we can write
 $ \angle y + \angle QSR = 90^\circ $
By using equation (2), we can simplify the above equation as,
 $ \angle y + {37^0} = 90^\circ $
By simplifying it, we get
 $ \angle y = 53^\circ $ . . . . (3)
Now, in $ \Delta PQS $
Since, the sum of the angles of a triangle is $ {180^0} $ . We can write
 $ \angle QPS + \angle PQS + \angle PSQ = 180^\circ $
By substituting the values of each angles, we get
 $ {90^\circ } + x + 53^\circ = 180^\circ $
 $ \Rightarrow x = 180^\circ - 143^\circ $
 $ \Rightarrow \angle x = 37^\circ $
Hence, we got the values of $ x $ and $ y $ as, $ \angle x = 37^\circ $ and $ \angle y = 53^\circ $

Note: We can also use another approach to solve this question. We can use the alternate interior angle property of parallel lines to find the value of $ x $ . And then we can use this value of $ x $ to find the value of $ y $ by using the property that the sum of angles of a triangle is equal to $ {180^0} $ .