Question

In the given figure, $E$ is any point on median $AD$ of a $\Delta ABC$. Show that $area\;\left( {ABE} \right) = area\;\left( {ACE} \right)$.

Answer 1

Hint:In the solution we will use the concept of median which states that median divides a triangle into two triangles of equal area. The statistical median basically used when the large numbers of data are provided.

Complete step-by-step solution
Given: $ABC$ is a triangle with $AD$ as median that is $BD = CD$ and $E$ is any point on $AD$.

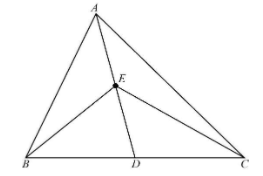
Since $AD$ is a median of $\Delta ABC$. Thus, it will divide $\Delta ABC$ into two triangles of equal area.
$area\;\left( {ABD} \right) = area\;\left( {ACD} \right)$……(1)
Also, $ED$ is a median of $\Delta ABC$. Thus, it will divide $\Delta ABC$ into two triangles of equal area.
$area\;\left( {EBD} \right) = area\;\left( {ECD} \right)$……(2)
Subtracting equation (2) from (1) we get
$\begin{array}{c}
area\;\left( {ABD} \right) - area\left( {EBD} \right) = area\;\left( {ACD} \right) - area\left( {ECD} \right)\\
area\;\left( {ABE} \right) = area\;\left( {ACE} \right)
\end{array}$
Therefore, $area\;\left( {ABE} \right) = area\;\left( {ACE} \right)$ is proved.

Note: Make sure to use the median of the triangle instead of statistical median. The median of the triangle tells us about the area of two triangles which are bisected by median. In a triangle, a median is the line which connects the vertex of a triangle with the midpoint of the line which is opposite to the vertex. The median in statics is used if the large numbers of data are given.