Question

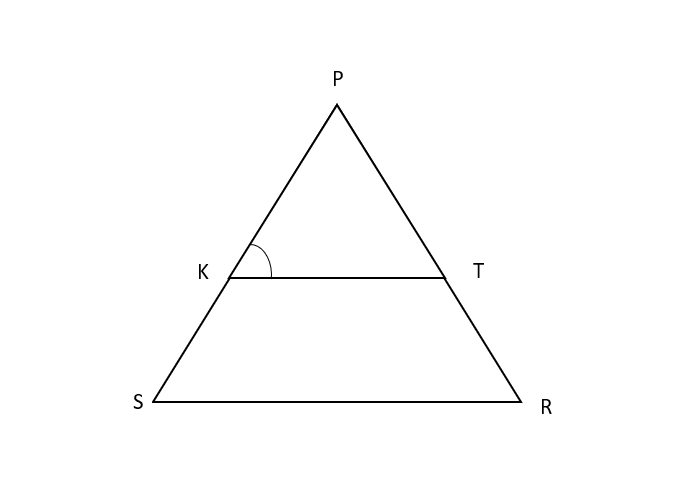
In the given figure, $\dfrac{{PK}}{{KS}} = \dfrac{{PT}}{{TR}}$ and $\angle PKT = \angle PRS$. Prove that $\Delta PSR$ is an isosceles triangle.

Answer 1

Hint: Try to solve using SAS congruence postulate.

Given: $\dfrac{{PK}}{{KS}} = \dfrac{{PT}}{{TR}}$ and $\angle PKT = \angle PRS$
To prove that $\Delta PSR$ is an isosceles triangle.
An isosceles triangle is a triangle with (at least) two equal sides.
Proof:
$\dfrac{{PK}}{{KS}} = \dfrac{{PT}}{{TR}}\left( {\because {\text{Given}}} \right)$
Rewriting above as:
$\dfrac{{KS}}{{KP}} = \dfrac{{RT}}{{PT}}$
Adding 1 both sides, we get
$
   \Rightarrow \dfrac{{KS}}{{KP}} + 1 = \dfrac{{RT}}{{PT}} + 1 \\
   \Rightarrow \dfrac{{KS + KP}}{{KP}} = \dfrac{{RT + PT}}{{PT}} \\
$
Now, from the figure, we can say that \[KS + KP = PS\] and \[RT + PT = PR\].
$\therefore \dfrac{{PS}}{{KP}} = \dfrac{{PR}}{{PT}}$
Now, $\angle KPT$ is common angle to $\Delta KPT$ and $\Delta SPR$
SAS congruence postulate states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then these two triangles are congruent and vice versa.
Using SAS similarity of triangles, $\Delta KPT \sim \Delta SPR$
$
   \Rightarrow \angle PKT = \angle PSR \\
   \Rightarrow \angle PRS = \angle PSR{\text{ }}\left( {\because \angle PKT = \angle PRS} \right) \\
$
Since, two angles of $\Delta PSR$are equal, it is an isosceles triangle.
Hence Proved.

Note: Whenever you need to prove sides as equal of a triangle, always try to prove triangles as similar. Also, we have the methods SSS (side-side-side), SAS (side-angle-side), ASA (angle-side-angle), AAS (angle-angle-side) and AAA (angle-angle-angle), to prove that two triangles are similar.