Question

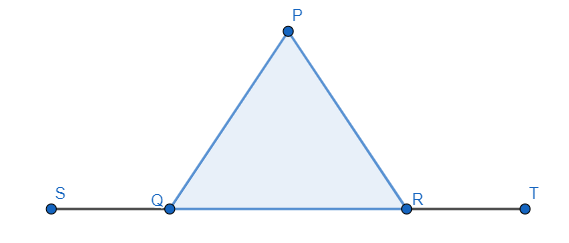
In the given figure $\angle PQR=\angle PRQ$ , then prove that $\angle PQS=\angle PRT$ .

Answer 1

Hint: Use the property that the sum of the linear pair of angles is equal to $180{}^\circ $ and it is clear from the diagram that angle PQS and angle PQR is a linear pair of angles.
Complete step-by-step answer:
To start with the solution, let us first describe a linear pair of angles. Linear pair of angles is defined as the pair of angles that have a common side and a common corner but don’t overlap each other and whose sum is equal to $180{}^\circ $ . We can show it in a diagram as:

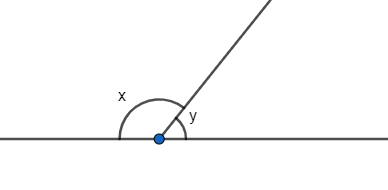
Using the concept of linear pair in our question, we get
$\angle PQR+\angle PQS=180{}^\circ $ , as angle PQR and angle PQS are linear pairs of angle.
Also, $\angle PRQ+\angle PRT=180{}^\circ $ , as angle PRQ and angle PRT are linear pairs of angle.
So, if we compare both the equations, we get
$\angle PQR+\angle PQS=\angle PRQ+\angle PRT$
Now, it is given in the question that $\angle PQR=\angle PRQ$ . So, if we use this in our equation, we get
$\angle PQR+\angle PQS=\angle PQR+\angle PRT$
$\Rightarrow \angle PQS=\angle PRT$
Hence, we have proved that $\angle PQS=\angle PRT$ .

Note: It is very important to learn all the properties of linear pair angles and adjacent angles as they are often used. Also, a point of similarity of all the pair of angles talked about in the above question is that they share the same vertex and the same intersecting lines.