Question

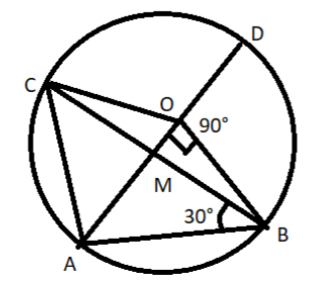
In the given figure, $\angle AOB=90{}^\circ $ and $\angle ABC=30{}^\circ $, Then $\angle CAD=?$

(a) $30{}^\circ $
(b) $45{}^\circ $
(c) $60{}^\circ $
(d) $90{}^\circ $

Answer 1

Hint: In triangle OAB, $\angle OAB=\angle OBA$, calculate $\angle OBA$. Assume point “M” as shown in the diagram. $\angle MBA=30{}^\circ $(given). Find $\angle MBC$ by subtracting $\angle MBA$ from $\angle OBA$. As OC=OB=r. So, \[\angle OCM=\angle OBM\]. Now calculate \[\angle COB\]and then calculate $\angle CAO$ by using the fact that “angle subtended by a chord at the center of a circle is double of the angle subtended by the chord at any point lying on the circle.”

Complete step-by-step solution:

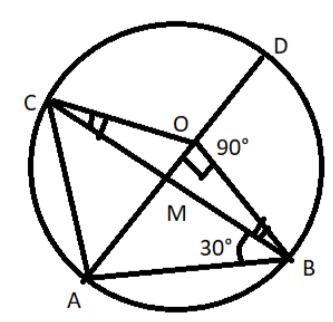
All the points are specified. Assume point of intersection of OA and BC on “M”.
In $\vartriangle OAB,\,OA=OB$=radius of the circle.
We know that if two sides is a triangle are equal, their corresponding angles will also be equal.
i.e. $\angle OAB=\angle OBA$
let \[\angle OAB=\angle OBA=x\]
By angle sum property of a circle, sum of the angles of a $\vartriangle $ is $180{}^\circ $.
In $\vartriangle $OAB-
$\begin{align}
  & \angle OAB+\angle OBA+\angle AOB=180{}^\circ \\
 & \Rightarrow x+x+90{}^\circ =180{}^\circ \\
 & \Rightarrow 2x=180{}^\circ -90{}^\circ \\
 & \Rightarrow 2x=90{}^\circ \\
 & \Rightarrow x=45{}^\circ \\
\end{align}$
So, $\angle OBA=\angle OAB=45{}^\circ $
From diagram,
$\begin{align}
  & \angle OBA=\angle OBM+\angle MBA \\
 & \Rightarrow 45{}^\circ =\angle OBM+30{}^\circ \\
 & \Rightarrow \angle OBM=45{}^\circ -30{}^\circ \\
 & \Rightarrow \angle OBM=15{}^\circ \\
\end{align}$
In $\vartriangle OCB$
OC=OB (both are radius of the circle)
So, corresponding angles will also be equal in the $\vartriangle $.
So, $\angle OCB=\angle OBC$
We have calculated above that $\angle OBM=15{}^\circ $
$\Rightarrow \angle OBC=15{}^\circ $ (see diagram)
So, $\Rightarrow \angle OBC=\angle OBM=15{}^\circ $
Now, in $\vartriangle $ OBM-
$\begin{align}
  & \angle MOB=90{}^\circ \,(given) \\
 & \angle OBM=15{}^\circ \,(calculated\,above) \\
\end{align}$
By angle sum property of triangle-
$\begin{align}
  & \angle MOB+\angle OBM+\angle OMB=180{}^\circ \\
 & 90{}^\circ +15{}^\circ +\angle OMB=180{}^\circ \\
 & \angle OMB=180{}^\circ -(90{}^\circ +15{}^\circ ) \\
 & \angle OMB=75{}^\circ \\
\end{align}$
By linear property straight lines on line BC-
$\begin{align}
  & \angle CMO+\angle OMB=180{}^\circ \\
 & \angle CMO+75{}^\circ =180{}^\circ \\
 & \left[ \angle OMB=75{}^\circ ,\,calculated\,above \right] \\
 & \angle CMO=180{}^\circ -75{}^\circ \\
 & \angle CMO=105{}^\circ \\
\end{align}$
Now in $\vartriangle OCM-$
$\begin{align}
  & \angle OCM=15{}^\circ (calculated\,above) \\
 & \angle OMC=105{}^\circ (calculated\,above) \\
\end{align}$
By angle sum property of a $\vartriangle $
$\begin{align}
  & \angle OCM+\angle OMC+\angle COM=180{}^\circ \\
 & \Rightarrow 15{}^\circ +105{}^\circ +\angle COM=180{}^\circ \\
 & \Rightarrow 120{}^\circ +\angle COM=180{}^\circ \\
 & \Rightarrow \angle COM=180{}^\circ -120{}^\circ \\
 & \Rightarrow \angle COM=60{}^\circ \\
\end{align}$
From the diagram, we can see that
$\begin{align}
  & \angle COB=\angle COM+\angle MOB \\
 & \angle COM=60{}^\circ \,(calcullated\,above) \\
 & \angle MOB=90{}^\circ \,(given) \\
 & So,\angle COB=60{}^\circ +90{}^\circ \\
 & \Rightarrow \angle COB=150{}^\circ \\
\end{align}$
We know that the angle subtended by a chord of a circle at its center is double the angle subtended by the chord at any point on its circumference.
We can see the diagram that chord BC subtends $\angle COB$ at the center of the circle and angle $\angle CAB$ at the circumference.
So,
$\begin{align}
  & \angle COB=2\times \angle CAB \\
 & \Rightarrow 150{}^\circ =2\times \angle CAB\,\,\,\left[ \angle COB=150{}^\circ \,as\,calculated\,above \right] \\
 & \Rightarrow \angle CAB=\dfrac{150{}^\circ }{2}=75{}^\circ \\
\end{align}$
From the diagram, we can see that $\angle CAB=\angle CAD+\angle OAB$
$\begin{align}
  & \angle CAB=75{}^\circ \,(calculated\,above) \\
 & \angle OAB=45{}^\circ \,(calculated\,above) \\
\end{align}$
So,
$\begin{align}
  & 75{}^\circ =\angle CAO+45{}^\circ \\
 & \Rightarrow \angle CAD=75{}^\circ -45{}^\circ =30{}^\circ \\
\end{align}$
Hence the required value of $\angle CAD$ will be $30{}^\circ $ and option (a) is the correct answer.

Note: We have used a theorem in the solution that the angle subtended by a chord at the center is double of the angle subtended by it on its circumference.
 

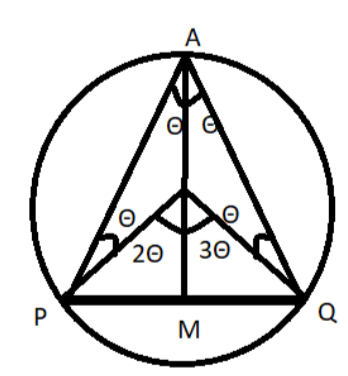
Given chord PQ of a circle subtending POQ at the centre O and PAQ at a point A n the circumference of the circle.
To prove:
$\angle POQ=2\angle PAQ$
Join AM such that AM is bisecting $\angle PAQ$
Let, $\angle PAD=\angle DAQ=\theta $
In $\vartriangle ADQ-OA=DQ\,(Both\,equal\,to\,radius)$
So, corresponding angles will also be equal.
i.e. $\angle OAQ=\angle OQA$
So, $\angle OQA=\theta $
Now by exterior angle sum property- (in $\vartriangle AOQ-$
$\begin{align}
  & \angle OAQ+\angle DQA=\angle MOQ \\
 & \Rightarrow \theta +\theta =\angle MOq \\
 & \Rightarrow \angle MOQ=2\theta \\
\end{align}$
Similarly, in $\vartriangle APO-$ (exterior angles property)
$\begin{align}
  & \angle POM=2\theta \\
 & Noq,\angle POQ=2\theta +2\theta =4\theta \,(See\,diagram) \\
 & and\,\angle PAQ=\theta +\theta =2 \\
\end{align}$
Hence, $\angle POQ=2\angle PAQ$