Question

In the given figure $ABCD$ is a trapezium in which $AB\parallel CD$ and $AD = BC$ . Show that
(i)$\angle A = \angle B$
(ii)$\angle C = \angle D$
(iii) $\Delta ABC \cong \Delta BAD$
(iv) diagonal $AC$= diagonal $BD$

Answer 1

Hint: To solve this problem, we will extend the line $AB$. Then we will use the properties of parallelogram to find the pair of equal sides. Also, whenever the two lines are parallel to each other and intersected by a transversal then the alternate angle formed by the transversal on the parallel lines are equal. We will also use the concept of linear pair as the sum of angles formed on a straight line are always supplementary. The concept of congruence is also used. We can say that the two triangles are congruent if they are the same in shape and size. Hence, in this question we will use the SAS congruence by comparing all the sides of the triangles formed.

Complete Step-by-step Solution
The following is the diagram of the trapezium ABCD.

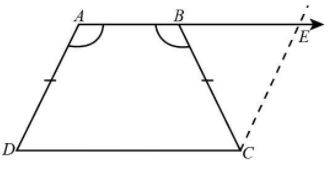
Given:
In the trapezium, $AB\parallel CD$ and $AD = BC$.
Construct a line $CE$ such that it is parallel to the line $AD$ and intersecting the extended line of $AB$ at point $E$ .

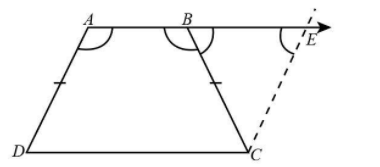
In ADCE, from the construction, $AD\parallel CE$
As $AE$ is the extension of line $AB$, therefore $AE\parallel CD$.

Since in ADCE, the pair of opposite sides are parallel, hence ADCE is a parallelogram.

We know that from the property of parallelogram, opposite sides of parallelogram are equal. Hence
$AD = CE$……(i)

Also as given in the question,
$AD = BC$……(ii)

On equating the equation (i) and (ii), we will get,
$BC = CE$

We know that from the property of triangles, we know that angles opposite to equal sides are always equal. Therefore,
$\angle CEB = \angle CBE$……(iii)

Since, we know $AD\parallel CE$ and $AE$ is the transversal. The interior angles on the same side of transversal is supplementary. Therefore,
$\begin{array}{c}
\angle A + \angle CEB = 180^\circ \\
\angle A = 180^\circ - \angle CEB
\end{array}$…..(iv)

Also, the sum of linear angle is always equals to $180^\circ $.
$\begin{array}{c}
\angle B + \angle CBE = 180^\circ \\
\angle B = 180^\circ - \angle CBE
\end{array}$……(v)
On equating the equation (iv) and (v), we will get,
$\angle A = \angle B$
Therefore, it is proved that $\angle A = \angle B$.

(ii)As $AB\parallel CD$and $AD$ is the transversal.

The interior angles on the same side of transversal is supplementary. Therefore
$\begin{array}{c}
\angle A + \angle D = 180^\circ \\
\angle D = 180^\circ - \angle A
\end{array}$…..(vi)

Also for $AB\parallel CD$and $BC$ is the transversal.
The interior angles on the same side of transversal is supplementary. Therefore
$\begin{array}{c}
\angle B + \angle C = {180^ \circ }\\
\angle C = {180^ \circ } - \angle B\,
\end{array}$

But as we have proved in the (i) solution, $\angle A = \angle B$.
$\angle C = {180^ \circ } - \angle A\,$ ……(vii)

On equating the equation (vi) and (vii), we will get,
$\angle C = \angle D$

Therefore, it is proved that $\angle C = \angle D$.

(iii)

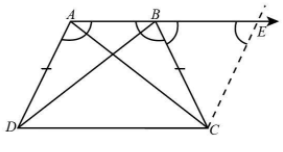
Consider $\Delta ABC$and $\Delta BAD$,
The common side is $AB$ , hence
$\begin{array}{c}
AB = BA\\
\angle A = \angle B\\
BC = AD
\end{array}$

Therefore, the triangles are congruent from the SAS congruence.
Also, we know by CPCT,
$\Delta ABC \cong \Delta BAD$

(iv)As it is proved earlier in (iii), $\Delta ABC \cong \Delta BAD$.
Therefore $AB = BD$ as it is the congruent part of the concurrent triangle.

Note: In this problem, make sure to use the mid-point theorem instead of other theorems when any question is asking about a quadrilateral with midpoints. The solution is totally based on the mid-point theorem. Mid-point is the point on the line segment which is exactly at the middle and it is equidistant from the end point of the line segment.