Question

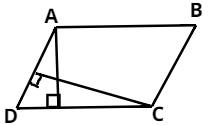
In the given figure, \[ABCD\] is a parallelogram, \[AE \bot DC\] and \[CF \bot AD\]. If \[AB = 16\;cm\],\[AE = 8\;cm\] and \[CF = 10\;cm\], find \[AD\].

Answer 1

Hint : Find area of parallelogram with the help of its two altitudes and equate them to get the required vale.

Given,
\[AB = CD = 16\;cm\] (Opposite sides of parallelogram)
We know,
\[CF = 10\;cm\] and \[AE = 8\;cm\]
Now we know,
Area of parallelogram = Base X Altitude
From the figure we can do this
\[CD \times AE = AD \times CF\]
On putting the value we get,
\[16 \times 8 = AD \times 10\]
We got $AD$ as,
\[
  AD = \dfrac{{128}}{{10}}\;cm \\
  AD = 12.8\;cm \\
\]

Note – In these types of questions of parallelogram, we should know the properties of parallelogram to solve the problem. Here we have used the properties that opposite sides of parallelogram are equal and area of parallelogram is base multiplied with altitude (Height).