Question

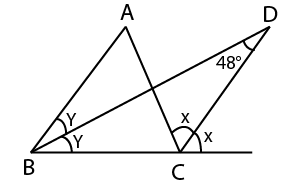
In the given figure, \[ABC\] is a triangle. The bisector of internal $\angle B$ and external $\angle C$ interest at $D$. If $\angle BDC = 48^\circ $, then what is the value (in degree) of $\angle A$?

Answer 1

Hint: This problem is based on the exterior angle theorem which states that in a triangle, the exterior angle is equal to the sum of two internal opposite angles. We will use the concept of exterior angle theorem and solve this problem.

Complete step-by-step answer:
Given a triangle \[ABC\] in which the bisector of internal $\angle B$ and external $\angle C$ interest at $D$.

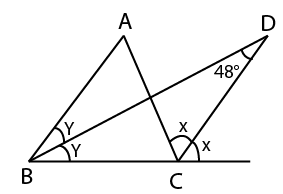
As we know that exterior angle is equal to the sum of two internal opposite angles.
Apply exterior angle property in $\Delta BCD$,
$\therefore \angle DCE = \angle DBC + \angle BDC$
$ \Rightarrow x = y + 48^\circ $
\[ \Rightarrow x - y = 48^\circ \]…..…….……(1)
Similarly, apply exterior angle property in$\Delta ABC$,
$\therefore \angle ACE = \angle BAC + \angle ABC$
$ \Rightarrow 2x = \angle A + 2y$
$ \Rightarrow 2x - 2y = \angle A$
$ \Rightarrow \angle A = 2\left( {x - y} \right)$
$ \Rightarrow \angle A = 2 \times 48^\circ $ [From (1)]
$ \Rightarrow \angle A = 96^\circ $

Therefore the value of $ \angle A$ is $96^\circ $

Note: This problem can also be solved as follows:
As we know that exterior angle is equal to the sum of two internal opposite angles.
Apply exterior angle property in $\Delta BCD$,
$\therefore \angle DCE = \angle DBC + \angle BDC$
$ \Rightarrow x = y + 48^\circ $
\[ \Rightarrow x - y = 48^\circ \]...........……(1)
As we know, the sum of interior angles of a triangle is $180^\circ $.
Apply angle sum property in $\Delta ABC$,
$\therefore \angle BAC + \angle ABC + \angle ACB = 180^\circ $
$ \Rightarrow \angle A + 2x + \left( {180 - 2y} \right) = 180^\circ $ $\left[ {\because \angle ACB = 180 - 2y} \right]$
$ \Rightarrow \angle A + 2x + 180 - 2y = 180^\circ $
$ \Rightarrow \angle A = 2x - 2y$
$ \Rightarrow \angle A = 2\left( {x - y} \right)$
$ \Rightarrow \angle A = 2 \times 48^\circ $ [From (1)]
$ \Rightarrow \angle A = 96^\circ $