Question

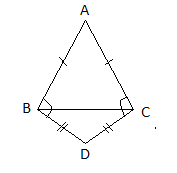
In the given figure, ABC and DBC are two isosceles triangles on the same base BC. Show that \[\angle ABC = \angle ACD\]

Answer 1

Hint: In an isosceles triangle, two sides are equal in length; hence its base angles are also equal.
A triangle is a polygon with three edges and three vertices, which are the basic shapes in geometry. It is a closed two-dimensional shape with three straight sides.
A triangle has three sides, and their type depends on the length of its sides and the size of its angles. There are basically three types of a triangle based on the length of the sides, namely: Scalene Triangle, Isosceles Triangle, and Equilateral Triangle.
An isosceles triangle is a triangle that has two sides of equal length. All the three angles of the isosceles triangle are acute angle, i.e., less than,\[{90^ \circ }\]whereas it’s the total sum of internal angle is \[{180^ \circ }\]

Complete step-by-step answer:
Given \[\vartriangle ABC\]is an isosceles triangle
Where \[AC = AB\]
Therefore \[\angle ABC = \angle ACB - - - (i)\]
[Since angle opposite to the equal sides of a triangle is equal]
Also \[\vartriangle BCD\] is an isosceles triangle
Where \[AC = AB\]
\[\angle DBC = \angle DCB - - - (ii)\]
[Since angle opposite to the equal sides of a triangle is equal]
Now add equation (i) and (ii), we get
\[\angle ACB + \angle DCB = \angle ABC + \angle DBC\]
In the figure since
\[\angle ABD = \angle ABC + \angle DBC\]
And
\[\angle ACD = \angle ACB + \angle DCB\]
Hence we conclude
\[\angle ABD = \angle ACD\]
Hence proved

Note: Another method to prove\[\angle ABD = \angle ACD\]in this question is by joining a line between the vertex A and D and proving the triangle ABD and ACD are equal and then showing\[\angle ABD = \angle ACD\] by CPCT.