Question

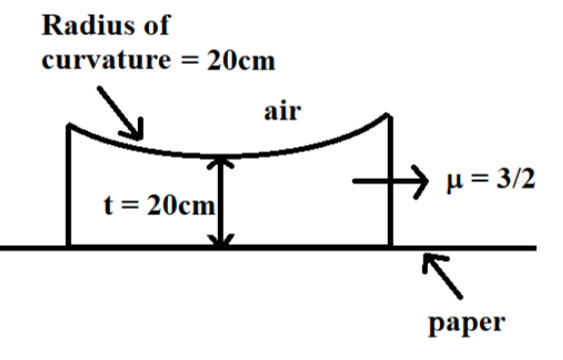
In the given figure, a plano-concave lens is placed on a paper on which a flower is drawn. How far above its actual position does the flower appear to be?

$A)10cm$
$B)15cm$
$C)50cm$
$D)$none of these

Answer 1

Hint: The thickness of the plano-concave lens is equal to the object distance. To determine the image distance for a plano-concave lens, we can use the formula for refraction through a concave surface. After refraction, the flower appears to be at a distance equal to the difference between the object distance and the image distance.

Formula used: For refraction through a concave surface,
$\dfrac{{{\mu }_{2}}}{v}-\dfrac{{{\mu }_{1}}}{u}=\dfrac{\left( {{\mu }_{2}}-{{\mu }_{1}} \right)}{R}$
where
${{\mu }_{1}}$ is the refractive index of the medium, through which light rays of an object pass towards the concave surface
${{\mu }_{2}}$ is the refractive index of the medium, through which light rays of the object pass after refraction from the concave surface
$u$ is the object distance
$v$ is the image distance
$R$ is the radius of curvature of the concave surface

Complete step-by-step solution:
A plano-concave lens is a type of lens, which has one concave surface. We are provided with a plano-concave lens, placed on a paper on which a flower is drawn. Image formation through this plano-concave lens can be related to the refraction through a concave surface because the lens is placed on the paper. The distance of the flower from the concave surface is equal to the thickness of the lens. At first, we intend to find the image distance of the flower.
Firstly, let us study the given diagram.
It is given that:
$R=20cm$, which is nothing but the radius of curvature of the lens
$t=20cm$, which is nothing but the thickness of the lens
$\mu =\dfrac{3}{2}$, which is nothing but the refractive index of the lens
Now, refraction through a concave surface is given by
$\dfrac{{{\mu }_{2}}}{v}-\dfrac{{{\mu }_{1}}}{u}=\dfrac{\left( {{\mu }_{2}}-{{\mu }_{1}} \right)}{R}$
where
${{\mu }_{1}}$ is the refractive index of the medium through which light rays from an object pass to the concave surface
${{\mu }_{2}}$ is the refractive index of the medium through which light rays from the object pass after refraction from the concave surface
$u$ is the object distance
$v$ is the image distance
$R$ is the radius of the concave surface
Let this be equation 1.
Let us use this equation to find the image distance of the flower through a plano-concave lens.
For that, let us take ${{\mu }_{1}}$ as the refractive index of the medium through which light rays from the flower pass to the concave surface and ${{\mu }_{2}}$ as the refractive index of the medium through which light rays pass after refraction from the concave surface.
Clearly,
${{\mu }_{1}}=\dfrac{3}{2}$
and
${{\mu }_{2}}={{\mu }_{air}}\approx 1$
From the question, it is also clear that
$R=20cm$
and
$u=t=20cm$
Substituting these values in equation 1, we have
$\dfrac{{{\mu }_{2}}}{v}-\dfrac{{{\mu }_{1}}}{u}=\dfrac{\left( {{\mu }_{2}}-{{\mu }_{1}} \right)}{R}\Rightarrow \dfrac{1}{v}-\dfrac{3}{2\times (-20)}=\dfrac{\left( 1-\dfrac{3}{2} \right)}{20}\Rightarrow \dfrac{1}{v}=\dfrac{-1}{40}-\dfrac{3}{40}=\dfrac{-4}{40}\Rightarrow v=-10cm$
Let this be equation 2. Note that refraction through a concave surface follows sign convention.
Therefore, the image distance of the flower is given by
$v=-10cm$
This suggests that the image is formed behind the concave surface, on the same side of the lens, where the flower is placed.
Finally, the distance between the actual flower and the image of the flower is given by
$v-u=-10-(-20)=10cm$
Therefore, the flower appears to be at a distance of $10cm$ from its actual position. The correct answer is given in option A.
The following diagram will give a clear idea of the above solution.

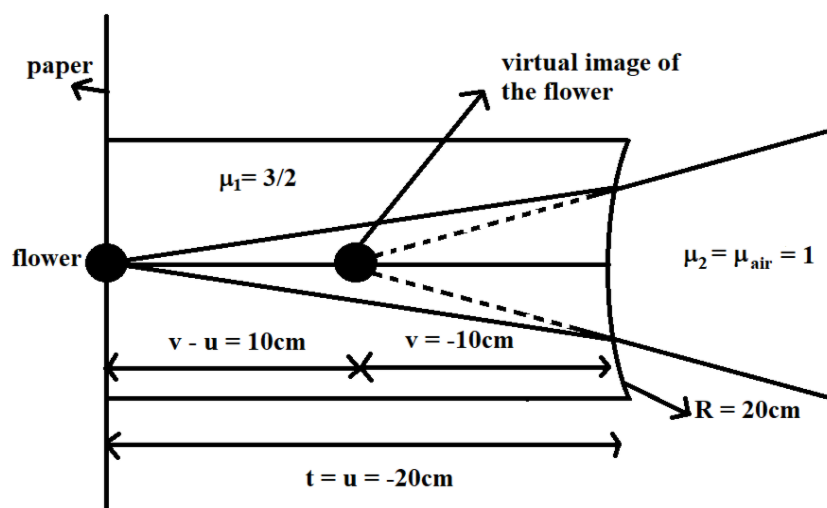
Note: Refraction through a concave surface follows sign convention. The parameters behind the concave surface are taken as negative while those in front of the concave surface are taken as positive, for easiness. Here, we have taken the distance of the flower from the concave surface as negative. At the same time, we have taken a radius of curvature of the concave surface as positive. After applying the formula, we got the image distance as negative, because it fell on the same side of the lens, where the object(flower) is kept.