Question

In the given electric circuit, the current flowing through the 3ohm resistor is 1ampere. Find the voltage of the battery and the circuit drawn from it.

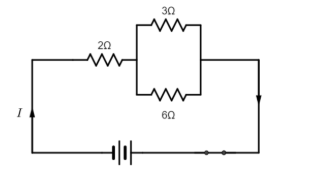
Answer 1

Hint: In a parallel combination of resistors, the current divides but voltage between the terminals is the same and reciprocal of the total resistance is the sum of the reciprocal of individual resistances.
In series combination of resistors voltage divides between two resistors but same current flows through them and effective resistance is the sum of the two resistances.

Complete step by step answer:

Consider circuit diagram, where ${{R}_{1}}=2\Omega ,{{R}_{2}}=3\Omega $ and ${{R}_{3}}=6\Omega $. Let ${{I}_{2}}=1A$ is the current flowing through ${{R}_{2}}$ as given in the question.

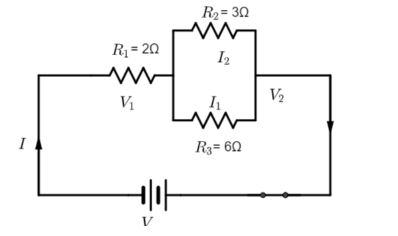
Now we have to find I and V which are total current and potential respectively.
Now first part to find total current I, we have,
$I={{I}_{1}}+{{I}_{2}}$ …….. (1)
we already know ${{I}_{2}}$ as it is given in question we have to find ${{I}_{1}}$
To find ${{I}_{1}}$ :
$I{}_{1}=\dfrac{{{V}_{2}}}{{{R}_{3}}}$ ….. (2)
the same voltage ${{V}_{2}}$ flows through ${{R}_{3}}$ as they are aligned parallel to each other.
but we don’t know ${{V}_{2}}$, it can be determined by using the formula:
${{V}_{2}}={{I}_{2}}{{R}_{2}}$ (Ohm’s law)
on substituting values of resistance and current we get,
${{V}_{2}}=1\times 3=3V$
On substituting ${{V}_{2}}$ in (2) we get
$\begin{align}
  & {{I}_{1}}=\dfrac{{{V}_{2}}}{{{R}_{3}}}=\dfrac{3}{6} \\
 & {{I}_{1}}=\dfrac{1}{2}A=0.5A \\
\end{align}$
Now we know both ${{I}_{1}}$and${{I}_{2}}$ substituting in (1) we get
$\begin{align}
  & I=1+0.5 \\
 & I=1.5A \\
\end{align}$
Thus, total current flowing through the circuit is found.
Now second part to find total potential V, we have,
$V={{V}_{1}}+{{V}_{2}}$ …… (3)
We know what is ${{V}_{2}}$ but have to find ${{V}_{1}}$ ,
${{V}_{1}}=I{{R}_{1}}$
on substituting I and ${{R}_{1}}$ we get
$\begin{align}
  & {{V}_{1}}=1.5\times 2 \\
 & {{V}_{1}}=3V \\
\end{align}$
on substituting values in (3)
$\begin{align}
  & V=3+3 \\
 & V=6V \\
\end{align}$
Thus, total potential of the circuit is found.

Note: Students should remember all the above formulas to solve this type of question.
Students may get confused about V and I which is constant, and which will vary when connected in series and parallel. Always remember that in series combination of resistors voltage divides current remains same between resistors and in parallel combination, the current divides but voltage remains constant.