Question

In the given circuit the current ${I_1}$ (magnitude only) is:

A. $0.4\,A$
B. $0.7\,A$
C. $0.8\,A$
D. None of these

Answer 1

Hint:Use the Kirchhoff’s laws to solve the circuit problem. Kirchhoff’s current law states that the algebraic sum of the currents meeting at a junction in an electrical circuit is zero.

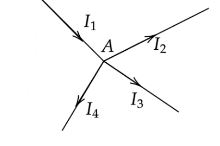
According to Kirchhoff’s Current law at the junction A in the above diagram,
$ - {I_1} + {I_2} + {I_3} + {I_4} = 0$
$\Rightarrow {I_1} = {I_2} + {I_3} + {I_4}$
The algebraic sum of incoming currents is equal to algebraic the sum of outgoing currents. Kirchhoff’s voltage law states that in any electrical circuit loop, the algebraic sum of all the electromotive forces and the voltage drops in resistors is equal to zero

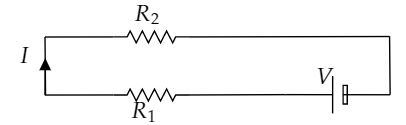
Apply Kirchhoff's voltage law in the above loop.
$ - I{R_1} - I{R_2} + V = 0$
$ \Rightarrow V = I{R_1} + I{R_2}$
The algebraic sum of all electromotive forces is equal to the algebraic sum of voltage drops across the resistors.

Complete step by step answer:
Let’s redraw the given diagram

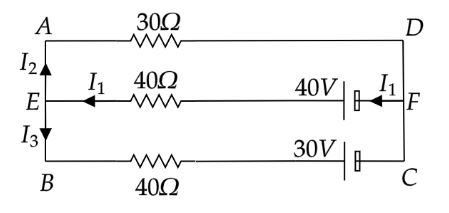
Apply Kirchhoff's Current law at the junction $E$ in the above circuit diagram.
${I_1} = {I_2} + {I_3}$
Now apply Kirchhoff’s voltage law in the loop $AEFD$.
$40{I_1} + 30{I_2} = 40$
$4{I_1} + 3{I_2} = 4$ …… (1)
Apply Kirchhoff’s voltage law in the loop $EBCF$.
$40{I_1} + 40{I_3} = 40 - 30$

Now substitute ${I_3} = {I_1} - {I_2}$ in the above equation.
$4{I_1} + 4\left( {{I_1} - {I_2}} \right) = 1$
$ \Rightarrow 8{I_1} - 4{I_2} = 1$
Further simplifying in terms of ${I_1}$
$ \Rightarrow {I_2} = 2{I_1}$
Substitute the value of ${I_2}$ in the above equation (1).
$4{I_1} + 3\left( {2{I_1}} \right) = 4$
Further calculating
$10{I_1} = 4$
$ \therefore {I_1} = 0.4\,A$

Hence, the correct option is $\left( A \right)$.

Note:While applying the Kirchhoff’s voltage law to a closed, algebraic sums are considered. Therefore, it is very important to assign proper signs to electromotive forces (e.m.f.) and voltage drops in the loop. A rise in potential should be considered positive and fall in potential should be considered as negative.