Question

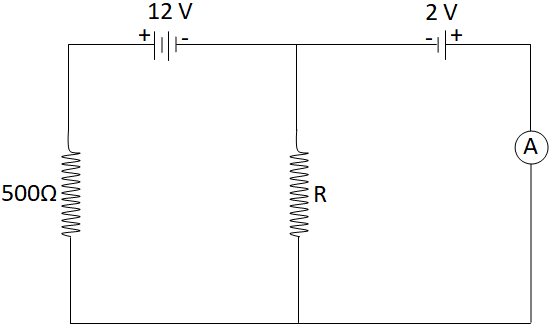
In the given circuit shown below, the ammeter reading is zero. Then the value of the resistance $R$ is:

Answer 1

Hint: In order to deal with this question first we will assume the current in the given circuit then we will proceed further by determining this current flowing through 500 ohm resistor further we apply ohm's law to get the value of unknown resistance.

Formula used- $V = IR$

Complete step-by-step solution -

Let's consider that , “i” is the current that passes through the circuit. In the specified circuit the reading of the ammeter is zero.
Hence, the voltage drop across $500\Omega $ resistance is $10V$ (as the batteries are oppositely connected).
As we know that according to the ohms law the relation between voltage, current and resistance is:
$
  V = IR \\
   \Rightarrow I = \dfrac{V}{R} \\
 $
So, the current through $500\Omega $ resistance is,
\[
  \because I = \dfrac{V}{R} \\
   \Rightarrow {I_{500\Omega }} = \dfrac{{10V}}{{500\Omega }} \\
   \Rightarrow {I_{500\Omega }} = \dfrac{1}{{50}}A \\
 \]
As we know that the current through the ammeter path is zero, so this current flowing through $500\Omega $ resistor must all be flowing through the resistor “R”.
\[
  \because {I_{500\Omega }} = \dfrac{1}{{50}}A \\
   \Rightarrow {I_R} = \dfrac{1}{{50}}A \\
 \]
And the voltage across the resistor “R” is 2V which is the same as the second cell.
As, now as we know the current and voltage across the resistor “R”; so, let us now use ohm’s law across the resistor “R” in order to find the value of resistance R.
$
  \because V = IR \\
   \Rightarrow R = \dfrac{V}{I} \\
   \Rightarrow R = \dfrac{{2V}}{{\left( {\dfrac{1}{{50}}A} \right)}} \\
   \Rightarrow R = 50 \times 2\Omega \\
   \Rightarrow R = 100\Omega \\
 $
Hence, the value of resistance is 100 ohm.

Note- Ohm's Law states that the current flowing through a conductor is directly proportional to the potential difference applied at its ends, provided the temperature and other physical conditions remain unchanged. Mathematically it can be represented as $V = IR$ . Ohm’s Law is used to determine the voltage, resistance or current of an electric circuit. Also it is used to maintain the desired voltage drop across the electronic components.