Question

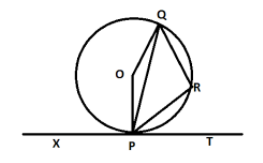
In the following figure, PQ is a chord of a circle with center O and PT is a tangent. If \[\angle QPT = 60^\circ \], then find $ \angle PRQ $.
               

Answer 1

Hint: To solve this problem, first we will obtain $ \angle OPT $ and then $ \angle POQ $ . From the later angle we will get $ \angle QPX $ . After that using the alternate segment theorem we will obtain $ \angle PRQ $ . It has an alternative method also.

Complete step-by-step answer:
Let X be a point left to the point O on tangent PT
According to the question it is given that,
The center of the circle is O.
PQ is a chord of the circle.
\[\angle QPT = 60^\circ \]
And, PT is a tangent to the circle at point P.
Hence, $ \angle OPT = 90^\circ $ ………..(1)
We can write $ \angle OPT $ as $ \angle OPQ + \angle QPT $ ,
Then the equation 1 becomes,
 $ \angle OPQ + \angle QPT = 90^\circ $
Putting \[\angle QPT = 60^\circ \]in the above equation we get,
 $ \angle OPQ + 60^\circ = 90^\circ $
 $ \Rightarrow \angle OPQ = 90^\circ - 60^\circ = 30^\circ $
 $ \vartriangle OPQ $ is an isosceles triangle as its two sides OP and OQ are equal (as both are the radius of the circle), and the angles in front of the equal sides are also equal. i.e. $ \angle OPQ = \angle OQP = 30^\circ $
And, PT is a tangent to the circle at point P.
Hence, $ \angle OPX = 90^\circ $
According to alternate segment theorem, the angle between a chord and tangent through one of the end points of the chord is equal to the angle in the alternate segment.
i.e. $ \angle PRQ = \angle QPX $
Thus by finding $ \angle QPX $ we will get $ m\angle PRQ $ .
We know that,
 $ \angle QPX = \angle OPX + \angle OPQ $
Putting the value of $ \angle OPX $ and $ \angle OPQ $ in the above equation we get,
 $ \angle QPX = 90^\circ + 30^\circ $
 $ \Rightarrow \angle QPX = 120^\circ $
Hence, $ \angle PRQ = 120^\circ $

Note: An isosceles triangle has its two sides are equal.
A chord of a circle is a straight line segment whose endpoints both lie on the circle.
Alternate segment theorem states that the angle between a chord and tangent through one of the end points of the chord is equal to the angle in the alternate segment.
In an alternative method, we will get minor arc POQ from step 4. And angle PRQ = half of the reflex angle of minor arc POQ i.e. half of the major arc PRQ.
An arc of the circle is the portion of the circumference of the circle.