Question

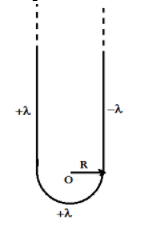
In the following figure, one semi-infinite wire and semi-circular arc is having linear charge density +λ and the other semi-infinite wire is having charge density −λ. Find the magnitude of electric field at point O:

(A). Zero
(B). \[\dfrac{{\sqrt 2 K\lambda }}{R}\]
(C). \[\dfrac{{2\sqrt 2 K\lambda }}{R}\]
(D). None of these.

Answer 1

Hint: For the above combination of the wires, two semi-infinite and one semi-circular will produce an electric field at point O, that will be the sum of all the three electric fields produced by the three types of wires. So, we will find the electric field produced by them separately along with their directions and then add all the three electric fields.

Complete step-by-step answer:
So, electric field produced by the semi-circular wire which is having linear charge density +λ =${\vec E_1} = K\dfrac{{\sqrt 2 \lambda }}{R}\hat i$
And the electric field produced by the semi-circular wire which is having linear charge density -λ= ${\vec E_1} = K\dfrac{{\sqrt 2 ( - \lambda )}}{R}\hat i$
Now we will calculate the and the electric field produced by the semi-circular arc which is having linear charge density +λ= ${\vec E_3} = \int\limits_0^{\dfrac{\pi }{2}} {2d{E_1}\sin \theta \hat j} $
$ \Rightarrow {\vec E_3} = 2\int\limits_0^{\dfrac{\pi }{2}} {K\dfrac{{\sqrt 2 \lambda }}{R}d\theta \sin \theta \hat j} $
$ \Rightarrow {\vec E_3} = \dfrac{{2\sqrt 2 K\lambda }}{R}\int\limits_0^{\dfrac{\pi }{2}} {\sin \theta d\theta \hat j} $
$ \Rightarrow {\vec E_3} = \dfrac{{2\sqrt 2 K\lambda }}{R}\left[ { - \cos \theta } \right]_0^{\dfrac{\pi }{2}}\hat j$
$ \Rightarrow {\vec E_3} = \dfrac{{2\sqrt 2 K\lambda }}{R}\left[ {( - \cos \dfrac{\pi }{2}) - ( - \cos 0)} \right]\hat j$
$ \Rightarrow {\vec E_3} = \dfrac{{2\sqrt 2 K\lambda }}{R}\hat j$
Thus, we have also found the electric field produced by the semi-circular arc.
So now the equivalent electric field at the point O is = $\vec E = {\vec E_1} - {\vec E_2} + {\vec E_3}$
So now substituting the values of all the three electric fields in the above equation, we get
$\vec E = K\dfrac{{\sqrt 2 \lambda }}{R}\hat i + K\dfrac{{\sqrt 2 ( - \lambda )}}{R}\hat i + \dfrac{{2\sqrt 2 K\lambda }}{R}\hat j$
$\vec E = K\dfrac{{\sqrt 2 \lambda }}{R}\hat i - K\dfrac{{\sqrt 2 \lambda }}{R}\hat i + \dfrac{{2\sqrt 2 K\lambda }}{R}\hat j$
$ \Rightarrow \vec E = \dfrac{{2\sqrt 2 K\lambda }}{R}\hat j$
Hence the electric field at the point O is $\dfrac{{2\sqrt 2 K\lambda }}{R}\hat j$, which is in the positive Y-direction.
And the magnitude of the field= $\left| {\vec E} \right| = \dfrac{{2\sqrt 2 K\lambda }}{R}$
So, option (C) is the correct answer.

Note: Here we have seen that the electric field at the centre of the semicircular arc is having some value. So, from this discussion we can have some more interesting results. One of them is that we can guess the result for the full circular ring of the wire. So when the semi-circular ring is having some value of the electric field then in the full circular ring the half of the hang will have the same value of the electric field and remaining semi-circular ring will also have the same magnitude of the electric field , but the direction of the electric fields of two halves of the circular ring will be opposite. Hence the resultant electric field at the centre of a circular ring will be zero.