Question

In the following figure, line M and line N are parallel. Which of the answer choices does NOT necessarily add up to $180^\circ $?

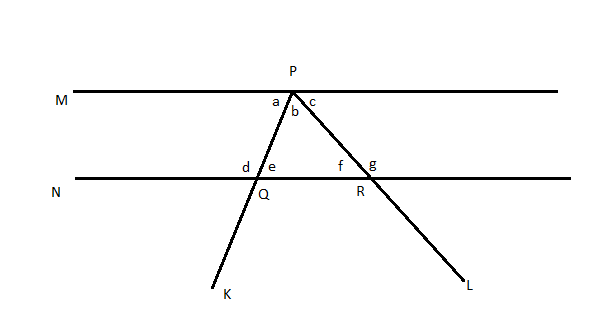
A. $\angle a + \angle b + \angle f$
B. $\angle a + \angle d$
C. $\angle b + \angle e + \angle f$
D. $\angle e + \angle g$

Answer 1

Hint: We have 2 parallel lines intersected by two transversals. Using the relations that corresponding angles are equal, vertically opposite angles are equal, alternate interior angles are equal and interior angles on the same side of the transversal are equal, we can compare the sum of each of the options to angle on a line or angle sum property of a triangle.

Complete step by step answer:

We have 2 parallel lines M and N cut by 2 transversals K and L which intersects line M at point P and line N at points Q and R. As we are asked to select the set of angles that add up to $180^\circ $, we can check through the sum of each option.
Consider option A, $\angle a + \angle b + \angle f$
Consider M and N cut by L, then $\angle f$and $\angle c$ are alternate interior angles and are equal.
$ \Rightarrow \angle f = \angle c$
Thus, we get,
$\angle a + \angle b + \angle f = \angle a + \angle b + \angle c$
Now the angles $\angle a$, $\angle b$ and $\angle c$ are angles on the line M. So, their sum is $180^\circ $.
Consider option B, $\angle a + \angle d$
Consider M and N cut by L, then $\angle a$ and $\angle d$ are exterior angles on the same side of the transversal and are supplementary.
$ \Rightarrow \angle a + \angle d = 180^\circ $
So, option B also adds up to $180^\circ $.
Consider option C,$\angle b + \angle e + \angle f$.
From the figure, these are the interior angles of the triangle PQR. Therefore, by angle sum property of triangle, $\angle b + \angle e + \angle f = 180^\circ $
So, option C also adds up to$180^\circ $.
Consider option D,$\angle e + \angle g$.
Consider the triangle PQR,
From the figure, $\angle g$ is an exterior angle of the triangle. Therefore, by exterior angle property,
$\angle g = \angle b + \angle e$…. (1)$180^\circ $
$\angle e + \angle g = 180^\circ $is possible only when $\angle e = \angle f$. As this condition is not given in the question and we cannot derive such condition, $\angle e + \angle g$ need not be.
So, the required answer is option D.

Note: When 2 parallel lines are intersected by a transversal, eight angles are formed.

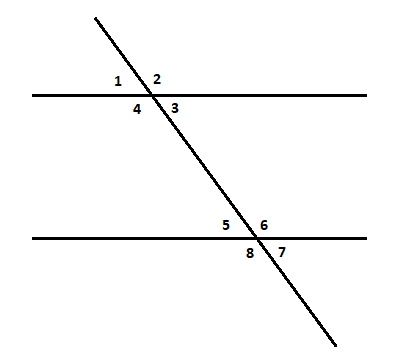
Then the corresponding angles will be equal, vertically opposite angles will be equal, Alternate interior angles will be equal, Interior angles on the same side of the transversal are supplementary.
Corresponding angles are the angles that have the same positions at each intersection.