Question

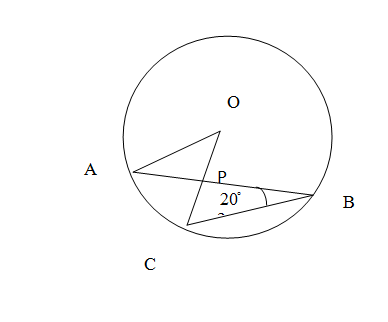
In the following figure if $\angle ABC={{20}^{\circ }}$, find $\angle AOC$\[\]

Answer 1

Hint: Extend BO which will cut the circle at say Q. We will get external angle $\angle AOQ$ for the triangle ABO and the angle $\angle COQ$ for the triangle CBO. Express them in terms of $\angle ABO,\angle CBO$ using the theorem that the external angle is the sum of two internal angles. Subtract $\angle AOQ$ from $\angle COQ$ to find $\angle AOC$. \[\]

Complete step-by-step answer:

We can see in the given figure that it is centred at O. There are two radii named OA and OC. As all the radii of a circle is of same length the OA=OC then. The arc AC subtends the angle $\angle ABC$ with a point B which lies on the circle whose measure is given in the question as $\angle ABC=20$\[\]
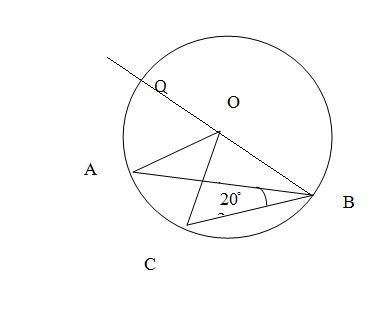
We name the point of intersection OC and AB as P and produce BO which cuts the circle at Q. Now BO is also a radius. So OB=OA. \[\]
Now we shall observe the triangle ABO. Here the two radii are equal, OA=OB. So their opposite angles will be equal. $\angle OAB=\angle OBA$. We know that the exterior angle is the sum of two opposite interior angles. So in triangle ABO we get the exterior angle $\angle AOQ$ .
\[\begin{align}
  & \angle AOQ=\angle OAB+\angle OBA \\
 & \Rightarrow \angle AOQ=\angle OBA+\angle OBA \\
 & \Rightarrow \angle AOQ=2\angle OBA...(1) \\
\end{align}\]
We again observe the triangle CBO. Here the two radii are equal, OC=OB. So their opposite angles will be equal. $\angle OCB=\angle OBC$. We know that the exterior angle is the sum of two opposite interior angles. So in triangle ABO we get the exterior angle $\angle COQ$

\[\begin{align}
  & \angle COQ=\angle OCB+\angle OBC \\
 & \Rightarrow \angle COQ=\angle OBC+\angle OBC \\
 & \Rightarrow \angle COQ=2\angle OBC....(2) \\
\end{align}\]
We subtract equation(1) from equation(2) and get
\[\begin{align}
  & \angle COQ-\angle AOQ=2\angle OBC-2\angle OBA \\
 & \Rightarrow \angle AOC=2\angle ABC=2\times {{20}^{\circ }}={{40}^{\circ }} \\
\end{align}\]
So the measure angle $\angle AOC$ is ${{40}^{\circ }}$.\[\]

Note: The problem can be shortly solved using the theorem “angle subtended at the centre by an arc is twice the angle subtended by it at the remaining part of the circle.” Here AB is the arc which has subtended angle $\angle ABC={{20}^{\circ }}$then its subtended angle at the centre will be twice of $\angle ABC$. So $\angle AOC=2\times {{20}^{\circ }}={{40}^{\circ }}$