Question

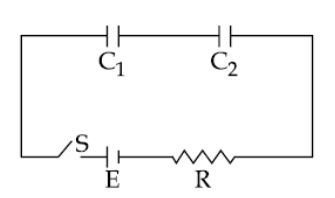
In the following circuit, the switch S is closed at t = 0. The charge on the capacitor C₁ as a function of time will be given by $\left( {{C_{eq}} = \dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}}} \right)$.

A $C_{eq}E[1-exp(-t/RC_{eq})]$
B $C_1E[1-exp(-t/RC_1)]$
C $C_2E[1-exp(-t/RC_2)]$
D $C_{eq}A exp(-t/RC_{eq})$

Answer 1

Hint: Capacitance is the ratio of the change in electric charge of a system to the corresponding change in its electric potential,$C = \dfrac{Q}{\varepsilon }$. Here charge Q changes with time and for an RC circuit can be written as Q(t)\[ = {Q_0}(1 - {e^{ - \dfrac{t}{\tau }}})\].

Complete step by step answer:
The figure shows a series RC circuit with a battery, resistor, and capacitors in series. The capacitor is initially uncharged, but starts to charge when the switch is closed. Initially the potential difference across the resistor is the battery emf, but that steadily drops (as does the current) as the potential difference across the capacitor increases.
Applying Kirchoff's loop rule:
$\varepsilon - IR - \dfrac{Q}{{{C_{eq}}}} = 0$
As Q increases I decreases, but Q changes because there is a current I. As the current decreases Q changes more slowly.
$I = \dfrac{{dQ}}{{dt}}$, so the equation can be written:
$\varepsilon - \dfrac{{dQ}}{{dt}}R - \dfrac{Q}{{{C_{eq}}}} = 0$
This is a differential equation that can be solved for Q as a function of time. The solution is
 Q(t)\[ = {Q_0}(1 - {e^{ - \dfrac{t}{\tau }}})\]
where ${Q_0} = {C_{eq}}\varepsilon $ and the time constant $\tau = R{C_{eq}}$.
Therefore, $Q(t) = \varepsilon {C_{eq}}(1 - {e^{ - \dfrac{t}{{R{C_{eq}}}}}})$

Therefore, option A is the correct answer.

Note:
Students should know to write the time varying equation of charge for a series RC circuit. The differential equation should be solved carefully without any mathematical mistake to avoid error in answer.Here $\tau $is the time constant of the RC circuit and is defined as the time required to charge the capacitor, through the resistance, by 63.2 percent of the difference between the initial value and final value or discharge the capacitor to 36.8 percent.