Question

In the figure which voltmeter reads zero, when $ \omega $ is equal to the resonant frequency of the series LCR circuit?

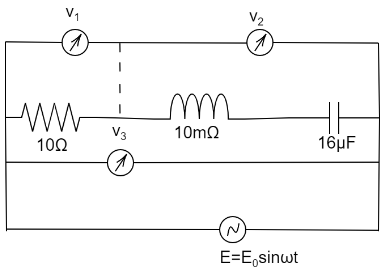
A). $ {V_1} $
B). $ {V_2} $
C). $ {V_3} $

Answer 1

Hint: An LCR circuit has three major components: resistor, inductor, capacitor.
These components can be connected in either a series or a parallel configuration.
Impedance is lowest at resonance in the LCR series. As a result, $ {Z_{\min }} = R $ . $ \omega $ is the angular frequency.

Complete Step By Step Answer:
A voltmeter will read zero when the points being measured are of the same potential.
Let the voltage across the inductor be $ {V_L} $ and voltage across the capacitor be $ {V_C} $ .
Voltage across the resistor is given by $ {V_1} = IR $ , where I is the current and R is the resistance.
Voltage across inductor and capacitor is given by $ {V_2} = {V_L} - {V_C} $
Therefore voltage across $ {V_3} $ is given by $ {V_3}^2 = {V_1}^2 + {({V_L} - {V_C})^2} $
Only the presence of resistor affect the voltage through the voltmeter $ {V_1} $ , the inductor and the capacitor affect the voltage through the voltmeter $ {V_2} $ , all three components affects the voltage through the voltmeter $ {V_3} $
Since the resonance voltage across the inductor and capacitor will be the same.
That is $ {V_L} = {V_C} $
 $ \Rightarrow {V_L} - {V_C} = 0 $
 $ \Rightarrow $ voltage across the voltmeter $ {V_2} $ will be zero.
The correct answer is option B, $ {V_2} $ .

Note:
The frequency at which the impedance of the LCR circuit becomes minimal or the current in the circuit becomes maximal is known as the resonance frequency.
Resonant frequency $ {\omega _r} = = \dfrac{1}{{\sqrt {LC} }} $
LCR circuits have a significant amount of resonance. Energy can be stored in LCR circuits in two ways: as an electric field in a capacitor when it is charged, or as a magnetic field in an inductor when current runs through it.