Question

In the figure, when the outer circles all have radii ‘r’ then the radius of the inner circle will be.

Answer 1

Hint:When we join all the points of larger circles they make a square and every three points make a right angled triangle. So, we will use the Pythagoras theorem to solve for a smaller radius.

Complete step-by-step answer:
Given: We have given the figure out of which all large circles have the same radius and we have to find the radius of the smaller circle.
First, we will join the center points of only three circles then it will make a right angled triangle.

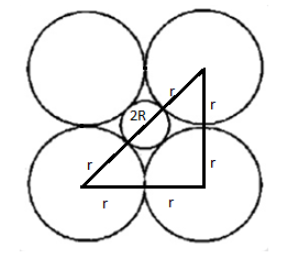
Now, let the radius of the smaller circle be R. Then the diameter of the smaller circle will be 2R.
In our triangle the length of base and height is equal to 2r because it is made up with the help of two radius of larger circles.
So the length of the hypotenuse will be the sum of the radius of outer 2 circles and the diameter of the inner circle, that is $2R+r+r=2R+2r$. And the height and the base of the triangle is the sum of the radius of two outer circles, that is, $r+r=2r$.
So, now, we will apply Pythagoras theorem in this right-angled triangle.
That is, $${\left(\text{hypotenuse}\right)}^2={\left(\text{height}\right)}^2+{\left(\text{base}\right)}^2$$
So, by putting all the values and simplify,
$$\begin{gathered} {\left(2R+2r\right)}^2={\left(2r\right)}^2+{\left(2r\right)}^2 \\ 4{\left(R+r\right)}^2=4{\left(r\right)}^2+4{\left(r\right)}^2 \\ {\left(R+r\right)}^2=2r^2 \\ {R}^2+r^2+2Rr=2r^2 \\ \Rightarrow R^2+2Rr-r^2=0 \end{gathered}$$
Now, we have got the quadratic equation and we will solve it by the quadratic root method which is$R={\displaystyle \frac{-B\pm \sqrt{{\left(B\right)}^2-4AC}}{2A}}$
But first we will compare the equation $R^2+2Rr-r^2=0$with the equation $A{R}^2+BR+C=0$because this equation is the standard equation for quadratic root method.
So, by comparing the equations we get, $A=1,B=2r,\text{ and }C=-r^2$
Now, put the values of A, B and C in the formula of the quadratic root equation.
Mathematically, $R={\displaystyle \frac{-\left(2r\right)\pm \sqrt{{\left(2r\right)}^2-4\left(1\right)\left(-r^2\right)}}{2\left(1\right)}}$
Now, solve this equation for $R$,
$$\begin{gathered} R={\displaystyle \frac{-\left(2r\right)\pm \sqrt{{\left(2r\right)}^2-4\left(1\right)\left(-r^2\right)}}{2\left(1\right)}} \\ ={\displaystyle \frac{-2r\pm \sqrt{4r^2+4r^2}}{2}} \\ ={\displaystyle \frac{-2r\pm \sqrt{8r^2}}{2}} \\ ={\displaystyle \frac{-2r\pm 2r\sqrt{2}}{2}} \\ ={\displaystyle \frac{2\left(-r\pm r\sqrt{2}\right)}{2}} \\ =\left(-r\pm r\sqrt{2}\right) \end{gathered}$$
Now, we will have two R one will be found by adding and the other will be found by subtracting.
$$\begin{gathered} R=\left(-r\pm r\sqrt{2}\right) \\ R=\left(-r-r\sqrt{2}\right),\left(-r+r\sqrt{2}\right) \\ R=-\left(1+\sqrt{2}\right)r,\left(\sqrt{2}-1\right)r \end{gathered}$$
So, we will take $R=\left(\sqrt{2}-1\right)r$because the other value is negative and a length can never be negative.
So, the radius of the smaller circle will be$$R=\left(\sqrt{2}-1\right)r$$.

Note:
The value of R can also be found by using the splitting middle method for solving the obtained quadratic method instead of quadratic formula, but it will be more complex than this, because roots are irrational.