Question

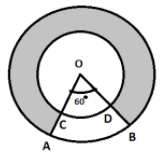
In the figure, two concentric circles with center O, have radii 21cm and 42cm. If $ \angle AOB = 60^\circ $ , find the area of the shaded region. [Use $ \pi = \dfrac{{22}}{7} $ ]

               

Answer 1

Hint: To solve the above question, first we will derive the area of the sector ABCD by subtracting the area of sector OCD from the area of the sector OAB. Then we will derive the area of the ring formed by both of the circles by subtracting the area of the inner circle from the area of the outer circle. And then subtracting area ABCD from the area of the ring we will get the area of the shaded region.

Complete step-by-step answer:
According to the question,
Radius of the inner circle, $ r = 21cm $
Radius of the outer circle, $ R = 42cm $
 $ \angle AOB = \theta = 60^\circ $
Hence, area of the sector OCD $ = \dfrac{\theta }{{360^\circ }}\pi {r^2} $
Putting the value of $ \theta ,r,\pi $ in the above equation we get,
 $ \therefore $ Area of the sector OCD $ = \dfrac{{60^\circ }}{{360^\circ }} \times \dfrac{{22}}{7} \times 21 \times 21 $
 $ = 231c{m^2} $
Similarly, area of the sector OAB $ = \dfrac{\theta }{{360^\circ }}\pi {R^2} $
Putting the value of $ \theta ,R,\pi $ in the above equation we get,
 $ \therefore $ Area of the sector OAB $ = \dfrac{{60^\circ }}{{360^\circ }} \times \dfrac{{22}}{7} \times 42 \times 42 $
 $ = 924c{m^2} $
 $ \therefore $ Area of the sector ABCD $ = 924 - 231 = 693c{m^2} $ …………………. (1)
Area of the ring formed by both of the circle will obtain by subtracting area of the inner circle from the area of the outer circle
i.e. The area of the ring = Area of outer circle – Area of inner circle
 $ = \pi {R^2} - \pi {r^2} $
 $ = \pi ({R^2} - {r^2}) $
Substituting the values of $ \pi ,R,r $ in the above equation we get,
The area of the ring $ = \dfrac{{22}}{7}({42^2} - {21^2}) $
 $ = \dfrac{{22}}{7}(1764 - 441) $
 $ = \dfrac{{22}}{7} \times 1323 $
 $ = 4158c{m^2} $ …………….. (2)
Hence, the area of the shaded region = Area of the ring – Area of the sector ABCD
Substituting equation 1 and 2 in the above equation we get,
The area of the shaded region $ = 4158 - 693 = 3465c{m^2} $
 $ \therefore $ The area of the shaded region is 3465 sq. cm.

Note: A circle is a shape consisting of all the points in a plane that are at a constant distance from a given point, called center. And the constant distance is called radius of the circle.
The circumference of a circle is given by $ 2\pi r $ , where r is the radius of the circle.
The area of a circle is given by $ \pi {r^2} $ .
If a ring is formed by two circles, then the area of the ring is $ = \pi ({R^2} - {r^2}) $ . Where R is the radius of the outer circle and r is the radius of the inner circle.
The area of the portion of a circle (arc) is $ = \dfrac{\theta }{{360^\circ }}\pi {r^2} $ , where $ \theta $ is the angle involved with that portion.
You should remember all the formulas related to the circle.
You might take the area of the shaded region by subtracting the area of the arc OAB and the area of the inner circle from the area of the outer circle. But it is wrong as it includes twice subtracting sector OCD.