Question

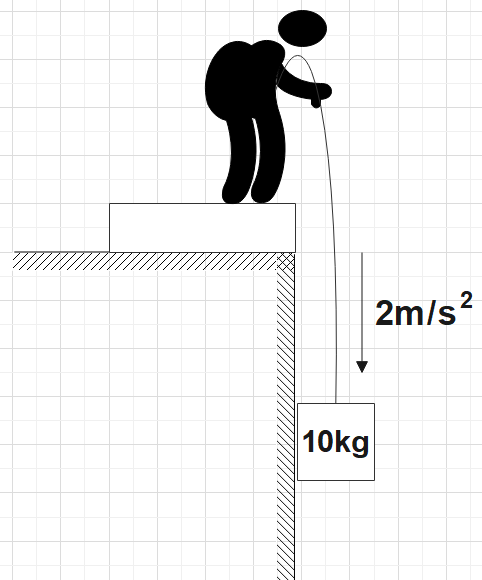
In the figure shown the man of mass 60kg is lowering a block of mass 10kg with an acceleration of $2m{{s}^{-2}}$. Find the reading of the machine.

Answer 1

Hint: As a very first step, one could read the question well and hence understand the whole system. After that you could make a free body diagram of the same. Now on balancing the forces by equating those acting in opposite directions, you will arrive at the answer.

Complete step by step answer:
In the question we are given the case of a man who is lowering a mass of 10kg standing on a machine with an acceleration of $2m{{s}^{-2}}$. The man who is doing this lowering of mass weigh 60kg. We are supposed to find the reading of the machine.
As a very first step, one could make a free body diagram of the given system.

Here, we see that the acceleration of the body is downwards and we could assign a pseudo force in the direction opposite to this, that is upwards. Now, we could find the net force as,
$mg-T=ma$
$\Rightarrow T=m\left( g-a \right)$
Substituting the values given, we get,
$T=10\left( 10-2 \right)=10\times 8$
$\therefore T=80N$
Therefore, we found the tension in the rope that is lowering the mass to be 80N. We conclude that the reading made by the machine will be of the tension in the string which is 80N.

Note: You may have noted that we have substituted the value of acceleration due to gravity to be $10m{{s}^{-2}}$where we know the value to be $9.8m{{s}^{-2}}$. This is done so as to make the calculation easier. Also, one should note that the weight of the man would in no way affect the tension in the rope and hence the reading.