Question

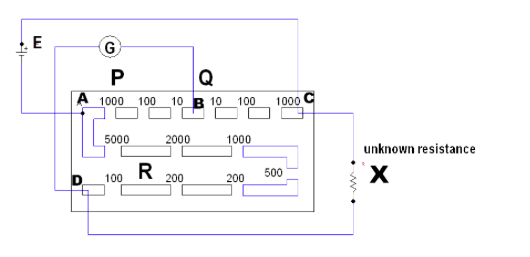
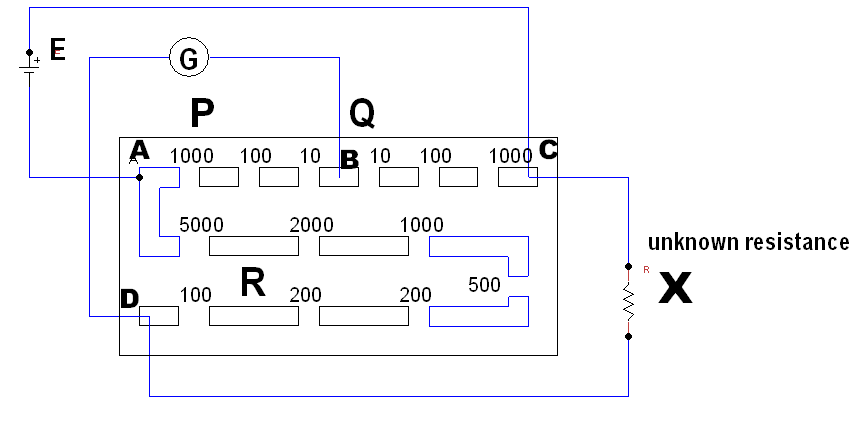
In the figure shown below, the maximum and the minimum possible unknown resistance\[\left( X \right)\], that can be measured by the post office box are \[{{\text{X}}_{\max }}\]is given by \[R \times {10^5}\]Ω, then \[R\] is : (In this experiment, we take out only one plugin arm \[AB\] and only one plugin arm\[BC\] , but in arms \[AD\] we can take out many plugs):

Answer 1

Hint:The post office box experiment is an application for a wheatstone bridge.
Wheatstone bridge: The Wheatstone Bridge was used to measure unknown resistance values and as a means of calibrating measuring instruments, voltmeters, ammeters, etc, by the use of a long resistive slide wire.
It was developed by Charles Wheatstone.

Formula Used:The condition for the Wheatstone bridge is
\[\dfrac{{\text{P}}}{{\text{Q}}} = \dfrac{{\text{X}}}{{\text{R}}}\]

Complete step by step answer:
To find the value of\[X\] ,
\[{\text{X = }}\dfrac{{\text{Q}}}{{\text{P}}}{\text{R}}\]

Through the above formula, we can find \[{{\text{X}}_{\max }}\]and \[{{\text{X}}_{\min }}\],
\[{{\text{X}}_{\max }} = \dfrac{{{Q_{\max }}}}{{{P_{\min }}}}{R_{\max }}\]
\[{{\text{X}}_{\min }} = \dfrac{{{Q_{\min }}}}{{{P_{\max }}}}{R_{\min }}\]
Firstly, let us find \[{{\text{X}}_{\max }}\]
\[{{\text{P}}_{\min }} = 10\] \[{{\text{R}}_{\max }} = 9000\] \[{{\text{Q}}_{\max }} = 1000\]
\[{{\text{X}}_{\max }} = \dfrac{{{Q_{\max }}}}{{{P_{\min }}}}\]
\[{R_{\max }} = \dfrac{{1000}}{{10}} \times 9000 = 900k\Omega \]
Now, let us find \[{{\text{X}}_{\min }}\]
\[{{\text{P}}_{\max }} = 1000\] \[{{\text{R}}_{\min }} = 100\] \[{{\text{Q}}_{\min }} = 10\]
\[{{\text{X}}_{\min }} = \dfrac{{{Q_{\min }}}}{{{P_{\max }}}}\]
\[{R_{\min }} = \dfrac{{10}}{{1000}} \times 100 = 1\Omega \]

\[{{\text{X}}_{\max }} = 900k\Omega \], \[{{\text{X}}_{\min }} = 1\Omega \]

Additional information:
The Wheatstone Bridge circuit is two simple series-parallel arrangements of resistances connected between a voltage supply terminal and ground terminal producing zero voltage difference between the two parallel branches when balanced. This circuit has two input terminals and two output terminals consisting of four resistors configured in a diamond-like arrangement.

Note:
-For closer measure, the denominator of R should be high then X will be minimum. Where the denominator of R is \[\dfrac{{\text{P}}}{{\text{Q}}}\].
-The Wheatstone bridge is used to measure the low resistance values precisely.
-This can also be used along with an operational amplifier to measure the physical parameters.
-We can also use it for measuring capacitance, inductance, and impedance.