Question

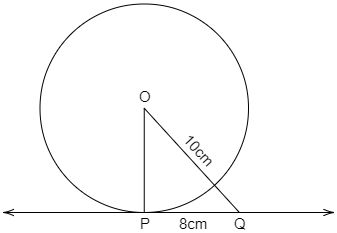
In the figure, PQ is tangent to the circle at P. Find the radius, if $PQ = 8cm$ and $OR = 10cm$.

Answer 1

Hint: To solve this question, we must have some basic knowledge of geometry, its identities, and also Pythagoras’s theorem. First of all, we will study the diagram of the above question which will make the solution of the question easier. From the diagram, we will see that the points O, P, and Q form a right-angled triangle, so we can simply find the length OP by applying Pythagoras’s theorem. This will be our final answer.

Step-By-Step answer:
First of all, we will see the diagram of the question which is given below,

Let us assume that the length OP is $x$.
As we can see in the above figure,
$ \Rightarrow OQ = 10cm,PQ = 8cm$
As we know, that the angle between the tangent and radius of a circle is the right angle.
$ \Rightarrow \angle OPQ = 90^\circ $
Now, we can see that the triangle has met all the requirements for applying Pythagoras’s theorem to it.
The formula of Pythagoras theorem is,
${h^2} = {p^2} + {b^2}$
Where $p = $ perpendicular
$b = $ base
$h = $ hypotenuse
So, applying Pythagoras’s theorem to the triangle as stated above, we can see that,
$ \Rightarrow {10^2} = {x^2} + {8^2}$
Square the terms,
$ \Rightarrow 100 = {x^2} + 64$
Move constant part on one side,
$ \Rightarrow {x^2} = 100 - 64$
Subtract the values,
$ \Rightarrow {x^2} = 36$
Taking square root on both sides,
$\therefore x = 6cm$

Hence, the radius is 6cm.

Note: To solve this question, don’t forget to make the diagram before solving as this will make solving the question easier. Also, for Pythagoras’s theorem, substitute the values of perpendicular, base, and hypotenuse carefully at the right place. Also, never become nervous if you don’t see a perfect square number inside the square root.