
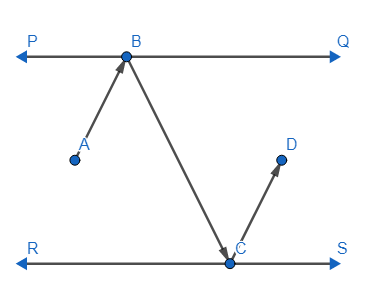
In the figure, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB ||CD.

Answer
601.5k+ views
Hint: First draw perpendiculars at the point of reflection then apply the law of reflection which states that angle of incidence is also angle of reflection. Then use the fact that if alternate interior angles are equal then lines are parallel to each other.
Complete step-by-step answer:
In the question, we are given a figure in which PQ, RS are two mirrors placed parallel to each other. Then we are shown an incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and reflects beach along CD.
Now we will do certain construction in the figure before solving
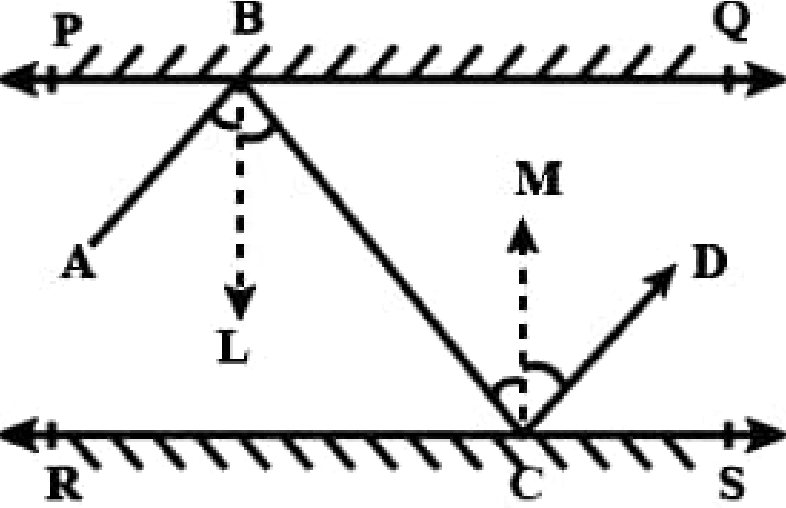
We will draw BL perpendicular to PQ, CM is perpendicular to RS, as PQ is parallel to RS so BL is parallel to CM.
Now as we know that BL is parallel to CM and BC is the transversal so we can say angle LBC= angle MCB as alternate interior angles is equal is a property.
Now we will apply the property that when an incident ray of light falls on a plane surface then its incident and reflected angle is equal. So by applying this we can say that,
Angle ABL = angle LBC
And angle MCB = angle MCD
As angle MCD = angle MCB and angle MCB = angle LBC
So, angle MCD = angle LBC
Now as angle MCB = angle LBC and angle LBC = angle ABL
So, angle MCD = angle ABL
And as we know that,
Angle LBC = angle MCB
So we can write,
Angle LBC + angle ABL = angle MCB + angle MCD
So we can write it as,
Angle ABC = angle BCD
These angles represent the alternate interior angles and as we proved that they are equal so we can tell that AB is parallel to CD.
Note: Students should know about properties of parallel lines, facts about the alternate interior angles and corresponding angles. They should also know for which condition we can prove two lines are parallel.
Complete step-by-step answer:
In the question, we are given a figure in which PQ, RS are two mirrors placed parallel to each other. Then we are shown an incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and reflects beach along CD.
Now we will do certain construction in the figure before solving
We will draw BL perpendicular to PQ, CM is perpendicular to RS, as PQ is parallel to RS so BL is parallel to CM.
Now as we know that BL is parallel to CM and BC is the transversal so we can say angle LBC= angle MCB as alternate interior angles is equal is a property.
Now we will apply the property that when an incident ray of light falls on a plane surface then its incident and reflected angle is equal. So by applying this we can say that,
Angle ABL = angle LBC
And angle MCB = angle MCD

As angle MCD = angle MCB and angle MCB = angle LBC
So, angle MCD = angle LBC
Now as angle MCB = angle LBC and angle LBC = angle ABL
So, angle MCD = angle ABL
And as we know that,
Angle LBC = angle MCB
So we can write,
Angle LBC + angle ABL = angle MCB + angle MCD
So we can write it as,
Angle ABC = angle BCD
These angles represent the alternate interior angles and as we proved that they are equal so we can tell that AB is parallel to CD.
Note: Students should know about properties of parallel lines, facts about the alternate interior angles and corresponding angles. They should also know for which condition we can prove two lines are parallel.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
What is the Full Form of ISI and RAW

What is the role of Mahatma Gandhi in national movement

What is the difference between Atleast and Atmost in class 9 maths CBSE

What were the main changes brought about by the Bolsheviks class 9 social science CBSE

Differentiate between the Western and the Eastern class 9 social science CBSE

Differentiate between parenchyma collenchyma and sclerenchyma class 9 biology CBSE




