Question

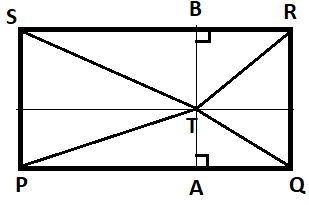
In the figure point $T$ is the interior of the rectangle $PQRS$.
Prove that $T{S^2} + T{Q^2} = T{P^2} + T{R^2}$
As shown in the figure, draw segment $AB\parallel PS$ and $ATB$.

Answer 1

Hint: First of all this is a very simple problem, and basic mathematics are needed here to solve this. In order to understand how to approach this problem, we have to know about the basic properties of a rectangle, and the properties of a right angled triangle. We should have an idea about the Pythagoras theorem, where if a right-angled triangle named ABC with hypotenuse AC and the other two sides AB and BC, then the Pythagoras theorem is given by:
$ \Rightarrow A{B^2} + B{C^2} = A{C^2}$

Complete step by step answer:
Given that there is a rectangle $PQRS$
Now $T$ is any interior point in the rectangle $PQRS$.
Now the AB line segment is parallel to PS and RQ.
The line segment AB is perpendicular to RS and PQ, as given below:
$ \Rightarrow AB \bot RS$ and $AB \bot PQ$
Now consider the triangle PTA, this is a right angled triangle. Hence it obeys the Pythagoras theorem, as given below:
$ \Rightarrow P{T^2} = P{A^2} + A{T^2}$
$ \Rightarrow P{T^2} - P{A^2} = A{T^2}$
Now consider the triangle ATQ, this is a right angled triangle. Hence it obeys the Pythagoras theorem, as given below:
$ \Rightarrow Q{T^2} = Q{A^2} + A{T^2}$
$ \Rightarrow Q{T^2} - Q{A^2} = A{T^2}$
From the above two expressions equating the $A{T^2}$ expressions, as given below:
$ \Rightarrow P{T^2} - P{A^2} = A{T^2}$
$ \Rightarrow Q{T^2} - Q{A^2} = A{T^2}$
$\therefore P{T^2} - P{A^2} = Q{T^2} - Q{A^2}$
Now consider the triangle SBT, this is a right angled triangle. Hence it obeys the Pythagoras theorem, as given below:
$ \Rightarrow S{T^2} = S{B^2} + B{T^2}$
$ \Rightarrow S{T^2} - S{B^2} = B{T^2}$
Now consider the triangle BRT, this is a right angled triangle. Hence it obeys the Pythagoras theorem, as given below:
$ \Rightarrow R{T^2} = R{B^2} + B{T^2}$
$ \Rightarrow R{T^2} - R{B^2} = B{T^2}$
From the above two expressions equating the $B{T^2}$ expressions, as given below:
$ \Rightarrow S{T^2} - S{B^2} = B{T^2}$
$ \Rightarrow R{T^2} - R{B^2} = B{T^2}$
$\therefore S{T^2} - S{B^2} = R{T^2} - R{B^2}$
From the rectangle it is clear that as AB is perpendicular to RS and PQ, which is given by:
$ \Rightarrow AB \bot RS$ and $AB \bot PQ$
$\therefore SB = PA$ and $RB = QA$
Substituting these expressions in the equation $S{T^2} - S{B^2} = R{T^2} - R{B^2}$, as given below:
$ \Rightarrow S{T^2} - P{A^2} = R{T^2} - Q{A^2}$
Now subtracting both the equations obtained, as given below:
$ \Rightarrow P{T^2} - P{A^2} = Q{T^2} - Q{A^2}$
$ \Rightarrow S{T^2} - P{A^2} = R{T^2} - Q{A^2}$
$ \Rightarrow P{T^2} - S{T^2} = Q{T^2} - R{T^2}$
Rearranging the terms gives:
$ \Rightarrow P{T^2} + R{T^2} = Q{T^2} + S{T^2}$
$\therefore T{S^2} + T{Q^2} = T{P^2} + T{R^2}$

Hence proved.

Note: While solving such kind of problems always Pythagoras theorem helps, which is important to keep that in mind. This problem can be done in the same way but slight changes, here instead of substituting the values of $SB = PA$ and $RB = QA$ in the second equation, and subtracting the two equations, we can substitute the values of $PA = SB$ and $QA = RB$ in the first equation, and subtract the resulting two equations to get the same result.