Question

In the figure, PC || QK, BC|| HK, AQ = 6cm, QH = 4cm, HP = 5cm and KC = 18cm.
Find AK and PB.

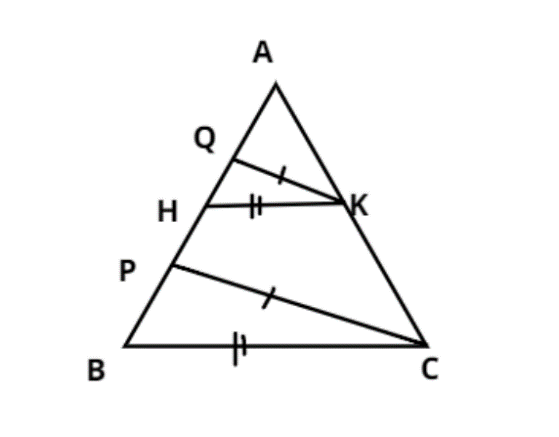
Answer 1

Hint – In this question use the concept of proportionality theorem, as PC || QK thus $\dfrac{{AQ}}{{QP}} = \dfrac{{AK}}{{KC}}$, and as HK || BC hence $\dfrac{{AH}}{{HB}} = \dfrac{{AK}}{{KC}}$. Moreover QP = QH + HP and AH = AQ + QH, this will help getting the right value of AK and PB.

Complete step-by-step answer:
Given data:
PC || QK, BC|| HK, AQ = 6cm, QH = 4cm, HP = 5cm and KC = 18cm.
According to the proportionality theorem of the triangle, if a line is drawn parallel to one of its sides of the triangle and it intersects the other two sides at two distinct points as shown in the given figure then it divides the two sides in the same ratio.
Therefore in triangle AQK and APC.
PC || QK (given)
$ \Rightarrow \dfrac{{AQ}}{{QP}} = \dfrac{{AK}}{{KC}}$
Now, QP = QH + HP = 4 + 5 =9cm
Now substitute the value we have,
$ \Rightarrow \dfrac{6}{9} = \dfrac{{AK}}{{18}}$
$ \Rightarrow AK = \dfrac{{6 \times 18}}{9} = 12$cm.
Now in the triangle AHK and ABC.
HK || BC
$ \Rightarrow \dfrac{{AH}}{{HB}} = \dfrac{{AK}}{{KC}}$................... (1)
Now, AH = AQ + QH = 6 + 4 =10cm.
HB = HP + PB = 5 + PB
Now substitute all the values in equation (1) we have,
 $ \Rightarrow \dfrac{{10}}{{5 + PB}} = \dfrac{{12}}{{18}}$
Now simplify this we have,
$ \Rightarrow 10 \times 18 = 12 \times \left( {5 + PB} \right)$
$ \Rightarrow 180 = 60 + 12PB$
$ \Rightarrow 12PB = 180 - 60 = 120$
$ \Rightarrow PB = \dfrac{{120}}{{12}} = 10$cm.
Therefore, AK = 12cm and PB = 10cm.
So this is the required answer.

Note – Understanding of diagrammatic representation always helps in figuring out the geometry involved in problems of such type. Proportionality theorem plays a vital role during solution and is applicable to any triangle no matter isosceles or equilateral if lines are drawn parallel to sides.