Question

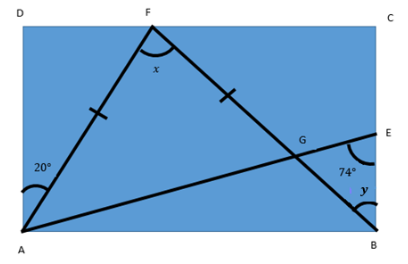
In the figure (not drawn to scale), ABCD is a rectangle, FA = FG, AGE and BGF are straight lines. Find $x + y$.

A) ${145^ \circ }$
B) ${124^ \circ }$
C) ${210^ \circ }$
D) ${116^ \circ }$

Answer 1

Hint: First of all we will see that $\angle D$ will be the right angle. Now we can find the $\angle AFD$ by applying angle sum property in $\vartriangle AFD$. Now, we can find the $\angle DAE$ using $\angle AEB$ as its alternate angle. Now, we can find $\angle FAG$ and $\angle FGA$ and thus the value of $x$ and then using the property of vertical angle to find the value of $y$.

Complete step-by-step answer:
We are given that ABCD is a rectangle. So, each angle will be a right angle.
Hence, $\angle D = {90^ \circ }$.
Now, consider $\vartriangle AFD$:
$\angle FAD + \angle D + \angle DFA = {180^ \circ }$ (Angle sum property) ……….(1)
[Angle sum property of triangle states that the sum of interior angles of a triangle is ${180^ \circ }$]
Now, we already have that: $\angle D = {90^ \circ }$ and $\angle FAD = {20^ \circ }$.
Putting these values in (1), we will get:-
$\angle DFA = {180^ \circ } - ({90^ \circ } + {20^ \circ }) = {70^ \circ }$ ………..(2)
Since AB and CD are the opposite sides of a rectangle.
Therefore they must be parallel.
Hence, $\angle DAE = \angle BEA$ (Alternate angles)
[Alternate angles are angles that are in opposite positions relative to a transversal intersecting two lines]
Therefore, we have $\angle DAE = {74^ \circ }$. …………(3)
Since, we see that $\vartriangle AFG$ is given to be isosceles and FA = FG.
Therefore, $\angle FAG = \angle FGA$ …………(4)
[Angles opposite to equal sides are equal]
We can clearly see in the figure that: $\angle DAE = \angle DAG = \angle DAF + \angle FAG$
Using (3) and (4) in this, we will get that:
$\angle FAG = \angle FGA = {54^ \circ }$ ………….(5)
Now, consider $\vartriangle AFG$:
$ \Rightarrow x + \angle FAG + \angle FGA = {180^ \circ }$ (Angle sum property)
Using (5) in this, we will get:-
$ \Rightarrow x + {54^ \circ } + {54^ \circ } = {180^ \circ }$
Simplifying this to get:-
$ \Rightarrow x = {72^ \circ }$ …………….(6)
Now, we see that $\angle FGA = \angle EGB$ (Vertically opposite angles)
[When two lines intersect they form two pairs of opposite angle, those angles are known as vertically opposite angles]
Using (5), we will get:
$\angle FGA = \angle EGB = {54^ \circ }$ ………..(7)
Now, let us consider $\vartriangle EGB$:
$\angle EGB + \angle GEB + \angle GBE = {180^ \circ }$ (Angle sum property)
Putting the values using given figure and (7), we will get:-
$ \Rightarrow {54^ \circ } + {74^ \circ } + y = {180^ \circ }$
$ \Rightarrow y = {180^ \circ } - {128^ \circ } = {52^ \circ }$ ………..(8)
Adding (6) and (8), we will get:
$x + y = {52^ \circ } + {72^ \circ } = {124^ \circ }$.

Hence, the correct option is (B).

Note: The students must not forget to write the reasons like Alternate angle, vertically opposite angle and Angle sum property because otherwise the solution may seem to be vague.
If the sum of two angles is 180, then they are called supplementary angles. If the sum of two angles is 90, then they are called complementary angles.