Question

In the figure given below, for an angle of incidence $45^\circ $ at the top surface, what is the minimum refractive index needed to total internal reflection at the vertical face?

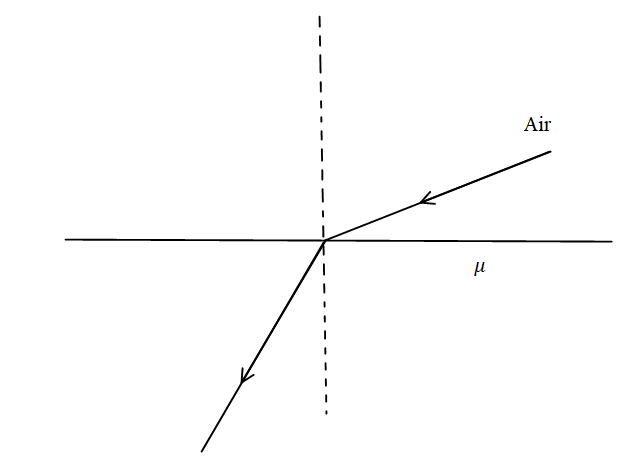
A. $\dfrac{{\sqrt 2 + 1}}{2}$
B. $\sqrt {\dfrac{1}{2}} $
C. $\sqrt {\dfrac{3}{2}} $
D. $\sqrt 2 + 1$

Answer 1

Hint: Snell's law can be used here for the calculation of minimum refractive index for this problem. According to Snell's law $\dfrac{{\sin i}}{{\sin r}} = \dfrac{{{n_2}}}{{{n_1}}}$, where $i$ is angle of incidence and $r$ is refracted angle and ${n_1}$is refractive index of medium 1 and ${n_2}$ is refractive index of medium 2.

Complete step by step solution:
Step 1:
It is given in the problem that the angle of incidence is $45^\circ $,
So, according to Snell's law,
\[
  \dfrac{{\sin i}}{{\sin r}} = \dfrac{{{n_2}}}{{{n_1}}} \\
  \dfrac{{\sin 45^\circ }}{{\sin r}} = \mu \\
  \sin r = \dfrac{1}{{\mu \cdot \sqrt 2 }} \\
 \]………eq.(1)
Step 2:
Total internal reflection is a phenomenon in which the light ray doesn’t show refraction while travelling from one medium to another medium but gets reflected into the same medium.
At the vertical wall let the angle of incidence be $i{'}$ and the angle of refraction is $90^\circ $ because for total internal refraction the angle of refraction should be more than or equal to $90^\circ $.
Applying Snell's law here,
$\dfrac{{\sin i{'}}}{{\sin r{'}}} = \dfrac{1}{\mu }$
Here $i{'}$ be the angle of incidence for vertical face and $r{'}$ be the angle of refraction for vertical face.
\[
  \dfrac{{\sin i{'}}}{{\sin r{'}}} = \dfrac{1}{\mu } \\
  \Rightarrow \dfrac{{\sin i{'}}}{{\sin 90^\circ }} = \dfrac{1}{\mu } \\
  \Rightarrow \mu \cdot \sin i{'} = \sin 90^\circ \\
  \Rightarrow \mu \cdot \sin i{'} = 1 \\
  \Rightarrow \sin i{'} = \dfrac{1}{\mu } \\
 \]………eq.(2)
Step 3:

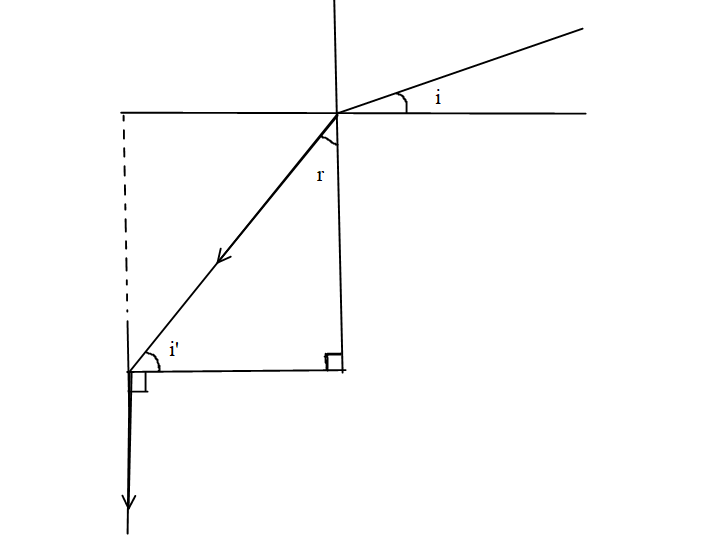
Here, in the triangle form, apply sum of angles of all the internal angle.
 $
  r + i{'} + 90^\circ = 180^\circ \\
  \Rightarrow r + i{'} = 90^\circ \\
 $
Writing in terms of $i{'}$,
$
  r + i{'} = 90^\circ \\
  \Rightarrow i{'} = 90^\circ - r \\
 $………eq.(3)
Step 4:
Replace the value of $i{'}$ from eq.(3) to eq.(2)
$\sin i{'} = \dfrac{1}{\mu }$
Put $i{'} = 90^\circ - r$ in above relation,
$
  \mu \cdot \sin i{'} = 1 \\
  \Rightarrow \mu \cdot \sin \left( {90^\circ - r} \right) = 1 \\
  \Rightarrow \mu \cdot \cos r = 1 \\
  \Rightarrow \cos r = \dfrac{1}{\mu } \\
 $………eq.(4)
Step 5:
Since,
${\sin ^2}r + {\cos ^2}r = 1$
Replacing the values of \[\sin r\] and $\cos r$ from equation (1) and (4),
$
  {\sin ^2}r + {\cos ^2}r = 1 \\
  {\left( {\dfrac{1}{{\mu \cdot \sqrt 2 }}} \right)^2} + {\left( {\dfrac{1}{\mu }} \right)^2} = 1 \\
  \Rightarrow \dfrac{1}{{2{\mu ^2}}} + \dfrac{1}{{{\mu ^2}}} = 1 \\
  \Rightarrow \dfrac{{1 + 2}}{{2{\mu ^2}}} = 1 \\
  \Rightarrow \dfrac{3}{{2{\mu ^2}}} = 1 \\
  \Rightarrow \mu = \sqrt {\dfrac{3}{2}} \\
 $
So the correct answer for this problem is $\mu = \sqrt {\dfrac{3}{2}} $. Hence option © is correct.

Note:
Students should note that the minimum value of refractive index is $\mu = \sqrt {\dfrac{3}{2}} $ which means if the value of refractive index is less than $\mu = \sqrt {\dfrac{3}{2}} $ then the light ray will not show internal reflection.