Question

In the figure given below:

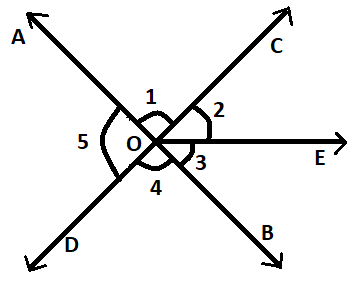
a). Is \[\angle 1\] adjacent to $\angle 2$?
b). Is $\angle AOC$ adjacent to $\angle AOE$?
c). Do $\angle COE$ and $\angle EOD$ form a linear pair?
d). Are $\angle BOD$and $\angle DOA$ supplementary?
e). Is $\angle 1$ vertically opposite to $\angle 4$?
f). What is the vertically opposite angle of $\angle 5$?

Answer 1

Hint: To solve this problem, we have to know about the concept of adjacent angles, supplementary angles, linear pair of angles, vertically opposite angles. Adjacent angles are those angles which are consecutive to each other. Supplementary angles are the angles which sum up to give ${180^ \circ }.$ Linear pair angles are those angles which are always supplementary. Vertically opposite angles are formed due to the intersection of two lines, these are also called as vertical angles which are always equal.

Complete step-by-step solution:
a). Is \[\angle 1\] adjacent to $\angle 2$?
Yes \[\angle 1\] adjacent to $\angle 2$, from the figure it is clearly evident that:
$ \Rightarrow \angle 1 = \angle AOC$, and
$ \Rightarrow \angle 2 = \angle COE$
From the figure it is clear that $\angle AOC$ is adjacent to $\angle COE$.
$\therefore \angle 1$ is adjacent to $\angle 2$.
b). Is $\angle AOC$ adjacent to $\angle AOE$?
We know that $\angle AOC = \angle 1$
From the given figure it is visible that $\angle AOE$ is the sum of two angles, as given below:
$ \Rightarrow \angle AOE = \angle AOC + \angle COE$
We already know that :
\[ \Rightarrow \angle AOC = \angle 1\], and
$ \Rightarrow \angle COE = \angle 2$
Here $\angle AOC$ is adjacent to $\angle COE$, but not adjacent to $\angle AOE$.
$\therefore \angle AOC$ is not adjacent to $\angle AOE$.
c). Do $\angle COE$ and $\angle EOD$ form a linear pair?
We know that a linear pair of angles are supplementary which means that they sum up to ${180^ \circ }$
Now consider $\angle COE$, from the figure it is clearly visible that:
$ \Rightarrow \angle COE = \angle 2$, and
From the given figure ,$\angle EOD$ is the sum of two angles, as given below:
$ \Rightarrow \angle EOD = \angle EOB + \angle BOD$
But we know that,
$ \Rightarrow \angle EOB = \angle 3$,
\[ \Rightarrow \angle BOD = \angle 4\]
Here the line CD, is a straight line, and a straight line has a linear angle of ${180^ \circ }$, as given below:
$ \Rightarrow \angle 2 + \angle 3 + \angle 4 = {180^ \circ }$
$ \Rightarrow \angle COE + \angle EOB + \angle BOD = {180^ \circ }$
We know that $\angle EOB + \angle BOD = \angle EOD$
$\therefore \angle COE + \angle EOD = {180^ \circ }$
Hence $\angle COE$ and $\angle EOD$ form a linear pair.
d). Are $\angle BOD$and $\angle DOA$ supplementary?
Here consider $\angle BOD$, from the above figure it is clear that:
$ \Rightarrow \angle BOD = \angle 4$
$ \Rightarrow \angle DOA = \angle 5$
Supplementary angles are those angles which sum upto ${180^ \circ }$, as given below:
$ \Rightarrow \angle 4 + \angle 5 = {180^ \circ }$
$\therefore \angle BOD + \angle DOA = {180^ \circ }$
Hence the angles $\angle BOD$and $\angle DOA$ supplementary.
e). Is $\angle 1$ vertically opposite to $\angle 4$?
When two lines intersect each other, then the opposite angles, formed due to intersection are called as vertical angles or vertically opposite angles.
Vertical opposite angles are always equal.
$ \Rightarrow \angle 1 = \angle 4$
$\therefore \angle 1$ and $\angle 4$ are vertically opposite angles.
f). What is the vertically opposite angle of $\angle 5$?
From the figure it is evident that the angle $\angle 5$ is given by:
$ \Rightarrow \angle 5 = \angle AOD$
Here the vertically opposite angle of $\angle AOD$ is $\angle COB$, as given below:
As already discussed the vertical angles are equal.
$ \Rightarrow \angle AOD = \angle COB$
But we know that $\angle COB$ is angle which is sum of two angles, which are given below;
$ \Rightarrow \angle COB = \angle COE + \angle EOB$
Here the angles $\angle COE,\angle EOB$ are given by:
$ \Rightarrow \angle COE = \angle 2$, and
$ \Rightarrow \angle EOB = \angle 3$
Here $\angle AOD = \angle 5$
Hence $\angle AOD$ is given by:
$ \Rightarrow \angle 5 = \angle 2 + \angle 3$
$\therefore $ The vertically opposite angle of $\angle 5$ is $\angle 2 + \angle 3$.

Note: Please note that there is a difference between linear pair of angles and supplementary angles. Linear pairs of angles are the two angles which are adjacent and share a common vertex, a linear pair forms a straight line which makes an angle of ${180^ \circ }$. But the supplementary angles need not be adjacent angles, any two angles which add up to give ${180^ \circ }$are called supplementary angles.