
In the figure below,
Answer
529.5k+ views
Hint: To find the value of PR, we will first consider the
Complete step-by-step solution
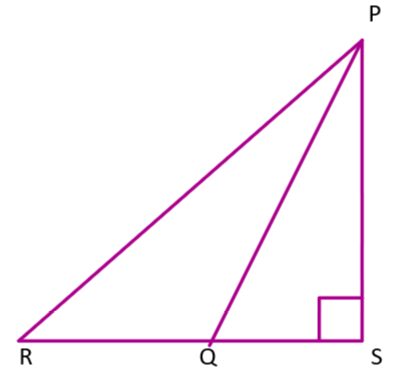
We have to find the value of PR. It is given that
Let us first consider the
Pythagoras theorem states that the square of the largest side of a triangle will be equal to the sum of squares of the other two sides.
It is given that
Let us substitute these values in equation (i). We will get
We can write this as
Now, let us take the square root.
Now, let us consider the triangle PRS. We can apply Pythagoras theorem here.
It is given that
Hence,
Let us now substitute the values. We will get
Now, we can substitute these values in equation (ii).
We will get
Now let us solve this. We will get
Let us take the square root. We get
Hence, the value of
Note: Pythagoras theorem must be thorough to solve these types of problems. Pythagoras theorem can be applied only when a triangle is a right-angled triangle. You may make an error in the Pythagoras theorem as
Complete step-by-step solution

We have to find the value of PR. It is given that
Let us first consider the
Pythagoras theorem states that the square of the largest side of a triangle will be equal to the sum of squares of the other two sides.
It is given that
Let us substitute these values in equation (i). We will get
We can write this as
Now, let us take the square root.
Now, let us consider the triangle PRS. We can apply Pythagoras theorem here.
It is given that
Hence,
Let us now substitute the values. We will get
Now, we can substitute these values in equation (ii).
We will get
Now let us solve this. We will get
Let us take the square root. We get
Hence, the value of
Note: Pythagoras theorem must be thorough to solve these types of problems. Pythagoras theorem can be applied only when a triangle is a right-angled triangle. You may make an error in the Pythagoras theorem as
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Indias first jute mill was established in 1854 in A class 10 social science CBSE

Five things I will do to build a great India class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE

10 examples of evaporation in daily life with explanations




