Question

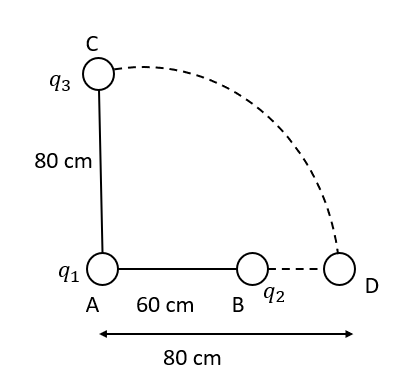
In the figure are shown charges $q_{1} = 2 \times 10^{-8} C$ and $q_{2} = -0.4 \times 10^{-8} C$. A charge $q_{3} = 0.2 \times 10^{-8} C$ is moved along the arc of a circle from C to D. The potential energy of $q_{3}$ is

a) will increase approximately by $76 \%$
b) will decrease approximately by $76 \%$
c) will remain same
d) will increase approximately by $12 \%$

Answer 1

Hint: An object possesses electric potential energy by two elements: the charge possessed by an object itself and the relative position of an object concerning other electrically charged objects. The measurement of electric potential depends on the value of work done in transferring the object from one location to another against the electric field.

Complete step-by-step solution:
Given: $q_{1} = 2 \times 10^{-8} C$
$q_{2} = -0.4 \times 10^{-8} C$
$q_{3} = 0.2 \times 10^{-8} C$
Initial potential energy on the $q_{3}$:
$U_{i} = \dfrac{k q_{3} q_{1}}{r_{13}} + \dfrac{k q_{3} q_{2}}{r_{23}}$
Final potential energy on the $q_{3}$:
$U_{f} = \dfrac{k q_{3} q_{1}}{r’_{13}} + \dfrac{k q_{3} q_{2}}{r’_{23}}$
Change in potential energy $= U_{f} -U_{i}$
$= \dfrac{k q_{3} q_{1}}{r_{13}} + \dfrac{k q_{3} q_{2}}{r_{23}} - \dfrac{k q_{3} q_{1}}{r’_{13}} - \dfrac{k q_{3} q_{2}}{r’_{23}}$
Put $r_{13} = r’_{13}$.
Therefore, change in potential energy will be:
$= \dfrac{k q_{3} q_{2}}{r_{23}} - \dfrac{k q_{3} q_{2}}{r’_{23}}$
Percentage of change in energy
$= \dfrac{ U_{f} -U_{i}}{U_{i}} \times 100$
$= \dfrac{\dfrac{k q_{3} q_{2}}{r_{23}} - \dfrac{k q_{3} q_{2}}{r’_{23}}}{\dfrac{k q_{3} q_{1}}{r_{13}} + \dfrac{k q_{3} q_{2}}{r_{23}}} \times 100$
$= \dfrac {q_{2}\left(\dfrac{ 1}{r_{23}} - \dfrac{1}{r’_{23}}\right)}{\dfrac{q_{1}}{r_{13}} + \dfrac{q_{2}}{r_{23}}} \times 100$
$r’_{23} = 0.2 m$, $r_{23} = 1 m$, $r_{13} = 0.8 m$
Put all the values in the above formula.
$= \dfrac {-0.4 \times 10^{-8} \left(\dfrac{ 1}{0.2} - \dfrac{1}{1}\right)}{\dfrac{2 \times 10^{-8} }{0.8} + \dfrac{-0.4 \times 10^{-8} }{1}} \times 100$
$= \dfrac {-0.4 \left(5-1\right)}{2.5-0.4} \times 100$
$= \dfrac{-1.6}{2.1} \times 100$
$= -76 \%$
So, Potential energy is decreased by $-76 \%$.
Option (b) is right.

Note:When an object is pushed against the electric field, it achieves some energy, described as the electric potential energy. For a charge, the electric potential is achieved by dividing the potential energy by the amount of charge.