Question

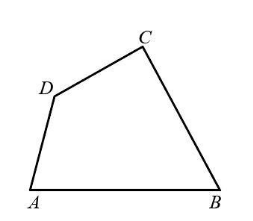
In the figure $ ABCD $ is a quadrilateral. Name a pair of opposite sides.

Answer 1

Hint: We basically define the shape of any object by the number of sides. A quadrilateral can be defined as a plane figure which has four edges and four corners or vertices. The four vertices are $ A $ , $ B $ , $ C $ and $ D $ . These four vertices are such that any three points can never be collinear..

Complete step-by-step answer:

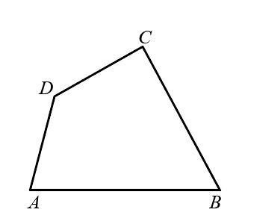
The given figure is a quadrilateral with four sides $ AB $ , $ BC $ , $ CA $ and $ AD $ . The four sides of the quadrilateral are such that they do not intersect each other except the end point. So, in order to find the opposite side of the quadrilateral we will make a pair of the sides which do not share a common endpoint.
 The given figure $ ABCD $ is a quadrilateral.
In the figure we will look for the pair of sides which do not share common end points. From the figure we have four sides $ AB $ , $ BC $ , $ CA $ and $ AD $ . The opposite sides are $ \left( {AB,CD} \right) $ and $ \left( {BC,DA} \right) $ as we can see in the figure that there is no common end points between $ AB $ and $ CD $ , and also between $ BC $ and $ DA $ .

Note: The given figure is a quadrilateral. If the quadrilateral were a parallelogram, then the pair of opposite sides must be parallel and equal to each other. The common mistake that can happen is considering a quadrilateral as a parallelogram. Since every parallelogram is a quadrilateral but not all the quadrilaterals are parallelograms. The sides which share a common endpoint are known as adjacent sides. In the given quadrilateral $ \left( {AB,BC} \right) $ , $ \left( {BC,CD} \right) $ , $ \left( {CD,DA} \right) $ and $ \left( {AD,AB} \right) $ are the adjacent sides.