Question

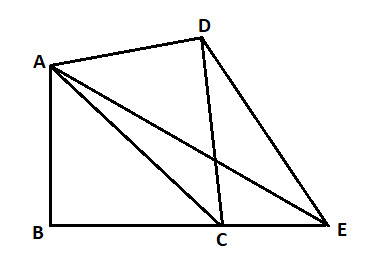
In the figure, ABCD is a quadrilateral. AC is the diagonal and $DE\left\| {AC} \right.$ also DE meets BC produced at E. Show that $ar(ABCD) = ar(\Delta ABE)$.

Answer 1

Hint: According to given in the question we have to show that $ar(ABCD) = ar(\Delta ABE)$ when ABCD is a quadrilateral. AC is the diagonal and $DE\left\| {AC} \right.$ also DE meets BC produced at E. So, first of all as mentioned in the question that AC is a diagonal and $DE\left\| {AC} \right.$also DE meets BC produced at E. therefore we can determine the two triangles which are in between the quadrilateral ABCD.
Now, we have to make both the triangles $\Delta DAC$ and $\Delta EAC$ which can be done by comparing the angles and sides of both of the triangles.
Now, we have to add the areas of both of the triangles $\Delta DAC$ and $\Delta EAC$ after that we have to add the area of the triangle $\Delta ABC$ in the area of the triangles we just obtained.

Complete step by step answer:
Step 1: First of all we as mentioned in the solution hint, that AC is a diagonal and $DE\left\| {AC} \right.$ also DE meets BC produced at E. Therefore we can determine the two triangles which are in between the quadrilateral ABCD. Hence,
$ \Rightarrow ar(ABCD) = ar(\Delta ABC) + ar(\Delta DAC)..............(1)$
Step 2: Now, we have to Now, we have to make the both the triangles $\Delta DAC$ and $\Delta EAC$ which can be done by comparing the angles and sides of the both of the triangles as we know that $\Delta DAC$ and $\Delta EAC$ lies on the same base and line DE is parallel to the line AC. Hence,
$ \Rightarrow ar(\Delta DAC) = ar(\Delta EAC)................(2)$
Step 3: Now, we have to add the area of the $\Delta ABC$ in the expression (2) as obtained in the solution step 2 according to mentioned in the solution hint,
$ \Rightarrow ar(\Delta DAC) + ar(\Delta ABC) = ar(\Delta EAC) + ar(\Delta ABC)$…………………..(3)
Step 4: Now, as we know that $\Delta DAC$ and $\Delta ABC$ is a quadrilateral ABCD and $\Delta EAC$ and $\Delta ABC$ is the triangle $\Delta ABE$. Hence, form the expression (3) as obtained in the solution step 3.
$ \Rightarrow ar(ABCD) = ar(\Delta ABE)$

Hence, we have proved that $ar(ABCD) = ar(\Delta ABE)$ when ABCD is a quadrilateral. AC is the diagonal and $DE\left\| {AC} \right.$ also DE meets BC produced at E.

Note: It is necessary to make both of the triangles $\Delta DAC$ and $\Delta EAC$ with the help of the AA rule in which we have to make to angles similar to each other to make the triangles congruent to each other to determine areas.
In the given quadrilateral ABCD there are two triangles which are $\Delta DAC$ and $\Delta ABC$ so the sum of areas of both of the triangles will be equal to the area of the quadrilateral ABCD.