Question

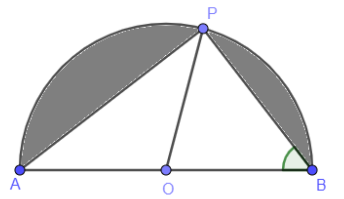
In the figure, a semi-circle with centre O is drawn on AB. The ratio of larger shaded area to the smaller shaded area is? $\Delta PBO=60{}^\circ $

(a) $\dfrac{4\pi -2\sqrt{3}}{2\pi -2\sqrt{3}}$
(b) $\dfrac{4\pi -3\sqrt{3}}{3\pi -3\sqrt{3}}$
(c) $\dfrac{4\pi -3\sqrt{3}}{2\pi -3\sqrt{3}}$
(d) $\dfrac{4\pi -2\sqrt{3}}{3\pi -2\sqrt{3}}$

Answer 1

Hint: First, we have only one angle given. We have to assume PO and OB as radius r so, angles opposite to this will be the same which will be 60. Then we have to find area of both the sector i.e. APO and BPO using the formula $=\dfrac{\theta }{360}{{r}^{2}}$ . Then we have to find the area to two triangles AOP and BOP out of which one will be an equilateral triangle and for the second triangle we have to calculate the area using some calculations needed. After finding areas of the triangle we will subtract it from the area of sector and taking ratio we will get the answer.

Complete step-by-step solution -
Here, we can consider radius r as $OP=OB=r$ . So, the angle opposite to OP is 60 degrees which will be the same as $\angle OBP$ which will be $\angle OPB=60{}^\circ $ .
Therefore, $\angle POB=60{}^\circ $ . So, triangle BOP is an equilateral triangle.

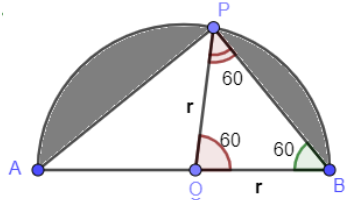
So, $\angle AOP+\angle POB=180{}^\circ $ will be a linear pair. So, from this we will find $\angle AOP$ which will get obtained as $\angle AOP+60{}^\circ =180{}^\circ \Rightarrow \angle AOP=120{}^\circ $
So, the area of sector APO $=\dfrac{\theta }{360} \pi{{r}^{2}}$ . Here, $\theta =120{}^\circ $ So, substituting the value we get,
Area of sector $APO=\dfrac{120}{360}\pi{{r}^{2}}=\dfrac{1}{3}\pi{{r}^{2}}$ …………………………………(1)
Now, for finding the area of sector PBO. We get
Area of sector $BPO=\dfrac{60}{360}\pi{{r}^{2}}=\dfrac{1}{6}\pi{{r}^{2}}$ …………………………………(2)
Now, finding the area of triangle POB, where we know that the height of the equilateral triangle will be $\dfrac{\sqrt{3}}{2}r$ .
$\therefore \text{area of }\Delta \text{BOP}=\dfrac{1}{2}\times base\times height$
$\therefore \text{area of }\Delta BOP=\dfrac{1}{2}\times r\times \dfrac{\sqrt{3}}{2}r=\dfrac{\sqrt{3}}{4}{{r}^{2}}$ ………………………(3)
Now, to find the area of triangle AOP is a little bit tricky. So, we will draw line OM perpendicular to base AP.

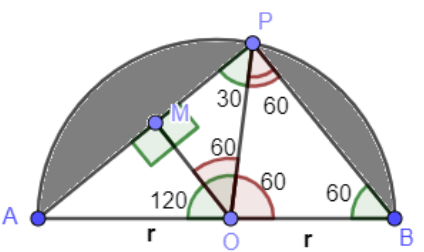
Here, OM is 90 degrees and the whole angle P is 90 degrees. But we know that $\angle BPO=60{}^\circ $ so, $\angle APO=90-60=30{}^\circ $ . Now, to find length of OM we take
$\cos 60=\dfrac{adjacent}{hypotenuse}=\dfrac{OM}{OP}$
$\dfrac{1}{2}=\dfrac{OM}{r}\Rightarrow OM=\dfrac{r}{2}$
Similarly, $\sin 60=\dfrac{opposite}{hypotenuse}=\dfrac{MP}{OP}$
On solving, we get
$\dfrac{\sqrt{3}}{2}=\dfrac{MP}{r}\Rightarrow MP=\dfrac{\sqrt{3}r}{2}$
So, now we get length of AP as
$AP=AM+MP=2MP=2\cdot \dfrac{\sqrt{3}r}{2}=\sqrt{3}r$
Therefore, area of $\Delta AOP=\dfrac{1}{2}\times AP\times OM=\dfrac{1}{2}\times \sqrt{3}r\times \dfrac{r}{2}$
$\text{area of }\Delta AOP=\dfrac{\sqrt{3}}{4}{{r}^{2}}$ ……………………….(4)
So, we have to find the ratio of shaded areas. Therefore, shaded area equal to area of sector minus area of triangle.
$=\left( \text{area of sector APO-area of }\Delta \text{AOP} \right):\left( \text{area of sector BPO-area of }\Delta B\text{OP} \right)$
So, Area of major shaded area : Area of minor shaded area
$=\left( \dfrac{1}{3}\pi {{r}^{2}}-\dfrac{\sqrt{3}}{4}{{r}^{2}} \right):\left( \dfrac{1}{6}\pi {{r}^{2}}-\dfrac{\sqrt{3}}{4}{{r}^{2}} \right)$
Taking ${{r}^{2}}$ common and cancelling out, we get
$=\dfrac{\left( \dfrac{1}{3}\pi -\dfrac{\sqrt{3}}{4} \right)}{\left( \dfrac{1}{6}\pi -\dfrac{\sqrt{3}}{4} \right)}$
Now, taking LCM and on solving we get
$=\dfrac{\left( \dfrac{4\pi -3\sqrt{3}}{12} \right)}{\left( \dfrac{4\pi -6\sqrt{3}}{24} \right)}$
$=\dfrac{\left( 4\pi -3\sqrt{3} \right)}{\left( \dfrac{4\pi -6\sqrt{3}}{2} \right)}$
$=\dfrac{\left( 4\pi -3\sqrt{3} \right)}{\left( 2\pi -3\sqrt{3} \right)}$
Thus, we got the ratio of major shaded part to the minor shaded part as $\dfrac{\left( 4\pi -3\sqrt{3} \right)}{\left( 2\pi -3\sqrt{3} \right)}$ .
Hence, option (c) is the correct answer.

Note: Be very careful while solving this type of sum. In finding all the angles it is very tricky and a bit confusing what to use where and which angle will come. Do not assume that O is the centre of circle so whole angle O will be 180 and then dividing it in 2 parts which become 90 degree each i.e. $\angle AOP=\angle BOP=90$ . From here, the whole answer will go wrong. So, do steps properly and carefully. Also, if one triangle is equilateral do not assume the second triangle to be equilateral. As done in the solution, we have to calculate the area of triangle AOP which coincidentally matches with the answer of area of the equilateral triangle. Every time it may not happen. So, do all the steps properly.