Question

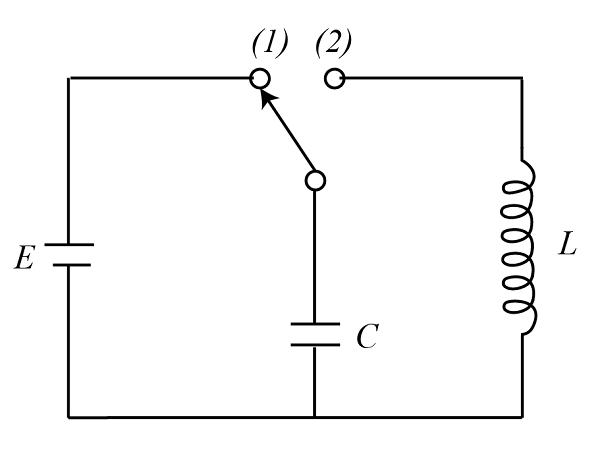
In the electrical network,  at t<0 (as given in the figure), key is placed on (1) till the capacitor got fully charged. Key is placed on (2) at t=0. Time when the energy in both the capacitor and the inductor will be same for the first time is

A) $\dfrac{\pi }{4}\sqrt {LC} $
B) $\dfrac{{3\pi }}{4}$$\sqrt {LC} $
C) $\dfrac{\pi }{3}$$\sqrt {LC} $
D) $\dfrac{{2\pi }}{3}$ $\sqrt {LC} $

Answer 1

Hint:A capacitor is a device that is used to store charges in an electrical circuit. At,  t<0 (as given in the figure), the capacitor will be fully charged and at the time of t=0 the inductor will have some charge and at that time capacitor will half of its maximum charge. Then charge q can be written as Q$\cos \omega t$ and $\omega $ =$\dfrac{1}{{\sqrt {LC} }}$ by these functions we will get the time of equal energy.

Step by step solution:
Step 1:
An inductor is a passive electronic component which is capable of storing electrical energy in the form of magnetic energy. Basically, it uses a conductor that is wound into a coil, and when electricity flows into the coil from the left to the right, this will generate a magnetic field in the clockwise direction.
A capacitor is a device that is used to store charges in an electrical circuit. A capacitor works on the principle that the capacitance of a conductor increases appreciably when an earthed conductor is brought near it. Hence, a capacitor has two plates separated by a distance having equal and opposite charges.
Step 2:
Energy stored in a capacitor is electrical potential energy, and it is thus related to the charge Q and voltage V on the capacitor.
The average voltage on the capacitor during the charging process is$\dfrac{v}{2}$, and so the average voltage experienced by the full charge q is $\dfrac{V}{2}$. Thus the energy stored in a capacitor, ${E_{CAP}}$ is,${E_{CAP}}$ =$\dfrac{Q}{V}$  where Q is the charge on a capacitor with a voltage V applied.
 (Note that the energy is not QV, but$\dfrac{{QV}}{2}$.) Charge and voltage are related to the capacitance C of a capacitor by Q = CV, and so the expression for ${E_{CAP}}$ can be algebraically manipulated into three equivalent expressions:
 ${E_{CAP}}$=$\dfrac{Q}{V}$=$\dfrac{{C{V^2}}}{2}$=$\dfrac{{{Q^2}}}{{2C}}$ where, Q is the charge and V the voltage on a capacitor C. The energy is in joules for a charge in coulombs, voltage in volts, and capacitance in farads.
Step 3:
At,  t<0 (as given in the figure), the capacitor will be fully charged and at the time of t=0 the inductor will have some charge and at that time capacitor will half of its maximum charge.
That means $\dfrac{{{q^2}}}{{2c}}$ =$\dfrac{{{Q^2}}}{{2C \times 2}}$
By solving this we will get q=$\dfrac{Q}{{\sqrt 2 }}$
Then, $Q\cos \omega t$ =$\dfrac{Q}{{\sqrt 2 }}$ ($\therefore $ cos$\dfrac{\pi }{4}$ =$\dfrac{1}{{\sqrt 2 }}$ )
To find the time of equal energies we can rewrite it as T=$\dfrac{\pi }{4}\sqrt {LC} $. (Remember $\omega $ =$\dfrac{1}{{\sqrt {LC} }}$ )

So option A. is correct

Note:One of the main differences between a capacitor and an inductor is that a capacitor opposes a change in voltage while an inductor opposes a change in the current. Furthermore, the inductor stores energy in the form of a magnetic field, and the capacitor stores energy in the form of an electric field.