Question

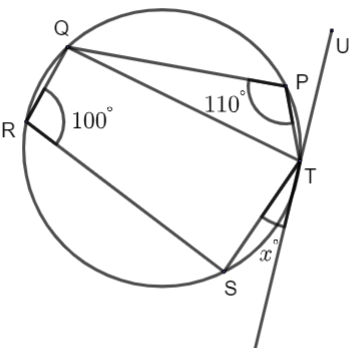
In the diagram, TU is a tangent to the circle at T. Find the value of x.

Answer 1

Hint: For solving this question you should know about the tangent to a circle. In this problem first we will discuss the tangent to a circle. And with the help of given triangles in the circle we will find the value of the rest angle which is given as \[{{x}^{\circ }}\].

Complete step by step solution:
According to the question it is given that TU is a tangent to the circle at T and asks the value of the angle.
So, we know that the circles and lines are two distinct shapes that have very little in common. But what happens if two of them meet or intersect at any single point? This gives rise to a tangent. A tangent to a circle is a line that touches the circle at a single point. The point to tangency is where the circle meets the point. A tangent is also perpendicular to the radius of the circle by which it intersects. It can be considered by a curved shape.
So, we can say that a line that joins two close points from a point on the circle is known as a tangent.
According to the diagram,
\[\angle STQ+\angle SRQ={{180}^{\circ }}\]
(RSTQ is a cyclic quadrilateral)
\[\therefore \angle STQ={{180}^{\circ }}-{{100}^{\circ }}={{80}^{\circ }}\]
By join QS
\[\angle QST+\angle QPT={{180}^{\circ }}\]
(PQST is a cyclic quadrilateral)
\[\therefore \angle QST={{180}^{\circ }}-{{110}^{\circ }}={{70}^{\circ }}\]
So, \[\angle QST+\angle SQT+\angle QTS={{180}^{\circ }}\]
(QST is a triangle)
\[\therefore \angle SQT={{180}^{\circ }}-\left[ {{80}^{\circ }}+{{70}^{\circ }} \right]\]
                                        \[={{180}^{\circ }}-{{150}^{\circ }}\]
                                        \[={{30}^{\circ }}\] (angles in the alternate segment)
So, the value of x is \[{{30}^{\circ }}\].

Note: There are various conditions of tendency only when a line touches the curve at a single point it is considered a tangent.
> When points lie on the circle.
> When a point lies inside the circle.
> When a point lies outside of the circle.