Question

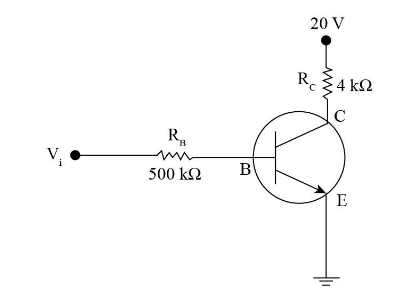
In the circuit shown in the figure, the input voltage \[{{\rm{V}}_{\rm{i}}}\] is 20 V, \[{{\rm{V}}_{{\rm{BE}}}} = 0\] and \[{{\rm{V}}_{{\rm{CE}}}} = 0\]. The values of \[{{\rm{I}}_{\rm{B}}}\],\[{{\rm{I}}_{\rm{C}}}\] and \[{\rm{\beta }}\] are given by

(1) \[{{\rm{I}}_{\rm{B}}} = 20\;{\rm{\mu A, }}{{\rm{I}}_{\rm{C}}} = 5\;{\rm{mA, \beta }} = 250\]
(2) \[{{\rm{I}}_{\rm{B}}} = 25\;{\rm{\mu A, }}{{\rm{I}}_{\rm{C}}} = 5\;{\rm{mA, \beta }} = 200\]
(3) \[{{\rm{I}}_{\rm{B}}} = 40\;{\rm{\mu A, }}{{\rm{I}}_{\rm{C}}} = 10\;{\rm{mA, \beta }} = 250\]
(4) \[{{\rm{I}}_{\rm{B}}} = 40\;{\rm{\mu A, }}{{\rm{I}}_{\rm{C}}} = 5\;{\rm{mA, \beta }} = 125\]

Answer 1

Hint:In the following question, the given circuit diagram is that of n-p-n bipolar junction transistor. The values for the base current, collector current and the current gain can be calculated by applying Kirchhoff’s law for each branch.

Complete step by step answer:
The input voltage is \[{{\rm{V}}_{\rm{i}}}\] = 20 V.
The voltage in BE is \[{{\rm{V}}_{{\rm{BE}}}} = 0\].
The voltage in CE is \[{{\rm{V}}_{{\rm{CE}}}} = 0\].
Applying Kirchhoff’s law to the lower branch of the circuit we have,
\[{{\rm{V}}_{\rm{i}}} = {I_{\rm{B}}}{R_{\rm{B}}} + {V_{{\rm{BE}}}}\]……(i)
On substituting the given values in the above equation we get,
\[\begin{array}{l}
20 = {I_{\rm{B}}} \times \left( {500 \times {{10}^3}} \right) + 0\\
{\rm{ }}{I_{\rm{B}}} = \dfrac{{20}}{{500 \times {{10}^3}}}\\
{\rm{ }}{I_{\rm{B}}} = 40\;{\rm{\mu A}}
\end{array}\]
Now, applying Kirchhoff’s law to the upper branch of the circuit we have,
\[{{\rm{V}}_{{\rm{CC}}}} = {I_{\rm{C}}}{R_{\rm{C}}} + {V_{{\rm{CE}}}}\]……(ii)
On substituting the given values in the above equation we get,
\[\begin{array}{l}
20 = {I_{\rm{C}}} \times \left( {4 \times {{10}^3}} \right) + 0\\
{I_{\rm{C}}} = \dfrac{{20}}{{4 \times {{10}^3}}}\\
{I_{\rm{C}}} = 5 \times {10^{ - 3}}{\rm{A }}\\
{I_{\rm{C}}}{\rm{ = 5}}\;{\rm{mA}}
\end{array}\]
The current gain value is the ratio of collector current (\[{I_{\rm{C}}}\]) to base current (\[{I_{\rm{B}}}\]). So, putting them all together we get,
\[\begin{array}{l}
{\rm{\beta }} = \dfrac{{{I_{\rm{C}}}}}{{{I_{\rm{B}}}}}\\
{\rm{\beta }} = \dfrac{{5 \times {{10}^{ - 3}}}}{{40 \times {{10}^{ - 6}}}}\\
{\rm{\beta }} = 125
\end{array}\]
Therefore, the values of the base current, collector current and the current gain are \[{{\rm{I}}_{\rm{B}}} = 40\;{\rm{\mu A, }}{{\rm{I}}_{\rm{C}}} = 5\;{\rm{mA, \beta }} = 125\] respectively, and option (D) is correct.

Note:The value of current gain is unit less as it is purely a ratio of the collector current to the base current. Also, the base current is always much smaller than the collector current, so we can say that the emitter current is nearly equal to the collector current. Generally, for a bipolar junction transistor to be in the on-state, the base-emitter junction needs to be in the forward biased condition while the collector-base junction needs to be reversed biased. The other category of BJTs (Bipolar Junction Transistors) PNP transistors operates in the same way as the NPN transistors. The only difference being there are flow of holes instead of electrons.