Question

In the circuit shown in the figure, the current through

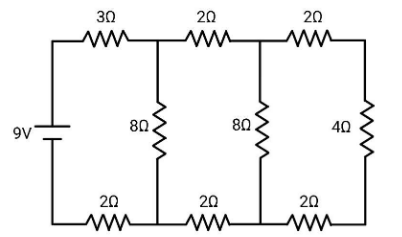
(A) the $3\Omega $ resistor is $0.5A$
(B) the $3\Omega $ resistor is $0.25A$
(C) the $4\Omega $ resistor is $0.5A$
(D) the $4\Omega $ resistor is $0.25A$

Answer 1

Hint: Any circuit may look large or might seem to be complicated, but in most cases, you can reduce the whole circuit and replace all the resistors with a single resistor. Or you can just reduce it to some resistors as per your convenience. This reduction is obtained by finding series and parallel combinations of resistors in the circuit. In the above circuit, find series and parallel combinations. Accordingly, find the current required.

Complete step by step answer:
As per the options available, we are supposed to find the current in the resistors $3\Omega $ and $4\Omega $.The resistors $2\Omega $, $4\Omega $ and $2\Omega $ in the right branch are in series. For resistances connected in series, the equivalent resistance is simply the sum of all the resistances in series. Mathematically, $R = {R_1} + {R_2} + {R_3} + ......$.So, we have equivalent resistances $2\Omega $, $4\Omega $ and $2\Omega $ as ${R_1} = 2 + 4 + 2 = 8\Omega $. If you consider the next branch having $8\Omega $ resistances (left of the rightmost branch), you can see that the resistance ${R_1}$ and this $8\Omega $ resistance are in parallel combination. For resistances connected in parallel, the reciprocal of the equivalent resistance is equal to the sum of the reciprocals of the resistances connected in parallel. Mathematically, $\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ......$.

So, we have equivalent of $8\Omega $ and ${R_1} = 8\Omega $ resistances as $\dfrac{1}{{{R_2}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{8}$
$\dfrac{1}{{{R_2}}} = \dfrac{1}{8} + \dfrac{1}{8} \\
\Rightarrow\dfrac{1}{{{R_2}}} = \dfrac{2}{8} = \dfrac{1}{4} \to {R_2} \\
\Rightarrow\dfrac{1}{{{R_2}}} = 4\Omega $
Now, this resistance is in series with the two $2\Omega $ resistances in the middle. So, their equivalent will be ${R_3} = 2 + 4 + 2 = 8\Omega $. Now, again this $8\Omega $ is in parallel with the leftmost $8\Omega $ resistance. So, their equivalent will be,
$\dfrac{1}{{{R_4}}} = \dfrac{1}{{{R_3}}} + \dfrac{1}{8} \\
\Rightarrow\dfrac{1}{{{R_4}}} = \dfrac{1}{8} + \dfrac{1}{8} = \dfrac{2}{8} \\
\Rightarrow\dfrac{1}{{{R_4}}} = \dfrac{1}{4} \\
\Rightarrow {R_4} = 4\Omega $
As you can see that we have reduced the circuit to a great extent. Now we have resistances ${R_4} = 4\Omega $, $3\Omega $ and $2\Omega $. These resistances are in series and therefore we can further reduce this to a single resistance. The overall equivalent resistance of the circuit is ${R_5} = 3 + 4 + 2 = 9\Omega $.

Now, according to Ohm’s Law, we have $V = IR$. $V$ being the voltage applied, in this case it is the emf of the battery, $I$ being the net current through the resistor, in this case the net current supplied by the battery, $R$ being the resistance, in this case the equivalent resistance ${R_5}$. So, the net current drawn from the battery will be given by,
$I = \dfrac{V}{R} \\
\Rightarrow I = \dfrac{{emf}}{{{R_5}}} \\
\Rightarrow I = \dfrac{9}{9} \\
\Rightarrow I = 1A$
Now, the net current which is supplied by the battery also enters back again in the battery.
If resistances are connected in series, the same amount of current will flow through each resistor and if resistances are connected in parallel, the current in each resistor may be different depending on the value of resistance.

The \[1A\] current flows through $3\Omega $ resistance, as it reaches the junction, it faces two resistances both of value $8\Omega $. As the potential across both resistances is the same since they are connected in parallel and even the resistances are equal, the current will be divided equally and will flow further. So, the current through $2\Omega $ (top one located in the middle, next to $3\Omega $) will be $0.5A$. Now this current will reach the next junction, and will again face two resistances of $8\Omega $ each. Again, the current will be divided equally and will flow further. So, $0.25A$ will flow in the $2\Omega $. As the $4\Omega $ resistor is in series, the same current will flow through it. So, $0.25A$ current will flow through $4\Omega $ resistor.

Hence, in the circuit shown in the figure, the current through the $4\Omega $ resistor is $0.25A$.Option D is correct.

Note: Always remember the method of reducing a particular set of resistances connected in series and parallel. Also remember how to calculate the equivalent resistances in case of series and parallel. Remember that when resistors are connected in series, the current will be the same in each and when the resistors are in parallel, the potential difference across each resistor will be the same.