Question

In the circuit shown in the figure, $R{\text{ }} = {\text{ }}\sqrt {\dfrac{L}{C}} $. Switch $S$ closed at time $t{\text{ }} = {\text{ }}0$. The current through $C$ and $L$ would be equal after a time $t$ equal to

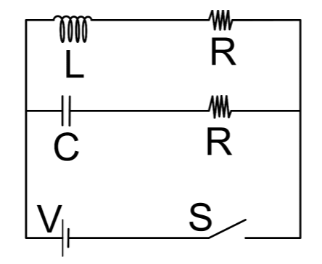
A. $CR\:$
B. $CR{\text{ }}\ln (2)\:$
C. $\dfrac{L}{{R{\text{ }}\ln (2)}}\:$
D. $LR\:$

Answer 1

Hint:We will first evaluate an equation of saturation current. Then, we will use the equation current flow through the capacitor and the inductor. Finally, we will equate the two and find the final answer by performing appropriate substitutions.

Formula used:
$I{\text{ }} = {\text{ }}\dfrac{V}{R}$
$I{\text{ }} = {\text{ }}{I_o}{\text{ }}{e^{\dfrac{{ - t}}{{RC}}}}$
$I{\text{ }} = {\text{ }}{I_o}{\text{ }}\left( {1{\text{ }} - {\text{ }}{e^{\dfrac{{ - Rt}}{L}}}} \right)$

Complete step by step answer:
The maximum current flowing in the circuit will be through the resistor. Thus,
${I_o}{\text{ }} = {\text{ }}\dfrac{V}{R}$
Now, the current flow through the capacitor is
${I_C}{\text{ }} = {\text{ }}{I_o}{\text{ }}{e^{\dfrac{{ - t}}{{RC}}}}$
Putting in the value of ${I_o}$, we get
${I_C}{\text{ }} = {\text{ }}\dfrac{V}{R}{\text{ }}{e^{\dfrac{{ - t}}{{RC}}}}$
Then, the current flow through the inductor, we get
${I_L}{\text{ }} = {\text{ }}{I_o}{\text{ }}\left( {1{\text{ }} - {\text{ }}{e^{\dfrac{{ - Rt}}{L}}}} \right)$
Putting in the value of \[{I_o}\], we get
${I_L}{\text{ }} = {\text{ }}\dfrac{V}{R}{\text{ }}\left( {1{\text{ }} - {\text{ }}{e^{\dfrac{{ - Rt}}{L}}}} \right)$

Now, as per the question the current through the capacitor and the inductor are equal.Thus, we equate the same, we get
$\dfrac{V}{R}{\text{ }}{e^{\dfrac{{ - t}}{{RC}}}}{\text{ }} = {\text{ }}\dfrac{V}{R}{\text{ }}\left( {1{\text{ }} - {\text{ }}{e^{\dfrac{{ - Rt}}{L}}}} \right)$
Canceling $V$ and $R$ on both sides, we get
${e^{\dfrac{{ - t}}{{RC}}}}{\text{ }} = {\text{ }}1{\text{ }} - {\text{ }}{e^{\dfrac{{ - Rt}}{L}}}{\text{ }} - - - - - - - - - - - - - - - {\text{ }}(i)$
Now, we are given that $R{\text{ }} = {\text{ }}\sqrt {\dfrac{L}{C}} $.
Substituting this value in ${e^{\dfrac{{ - Rt}}{L}}}$, we get
${e^{\dfrac{{ - \sqrt {\dfrac{L}{C}} {\text{ }}t}}{L}}}{\text{ }} - - - - - - - - - {\text{ }}(ii)$
We can write $L{\text{ }} = {\text{ }}\sqrt {{L^2}} $.
Thus, equation $(ii)$, we get
${e^{ - \sqrt {\dfrac{L}{{{L^2}C}}} {\text{ }}t}}$
Further, we get
\[{e^{ - \sqrt {\dfrac{1}{{LC}}} {\text{ }}t}}{\text{ }} - - - - - - - - - {\text{ }}(iii)\]

Now, we can write
\[\sqrt {\dfrac{1}{{LC}}} {\text{ }} = {\text{ }}\sqrt {\dfrac{1}{{\dfrac{L}{C}{\text{ }} \times {\text{ }}{C^2}}}} \]
That means we can write
$\sqrt {\dfrac{1}{{LC}}} {\text{ }} = {\text{ }}\dfrac{1}{{RC}}$
Thus, equation $(iii)$turns out to be
${e^{\dfrac{{ - t}}{{RC}}}}$
Substituting this in equation $(ii)$, we get
${e^{\dfrac{{ - t}}{{RC}}}}$
Thus, equation $(i)$ becomes
${e^{\dfrac{{ - t}}{{RC}}}}{\text{ }} = {\text{ }}1{\text{ }} - {\text{ }}{e^{\dfrac{{ - t}}{{RC}}}}$
Then, we can write
$2{\text{ }}{e^{\dfrac{{ - t}}{{RC}}}}{\text{ }} = {\text{ }}1$
Then, we get
${e^{\dfrac{{ - t}}{{RC}}}}{\text{ }} = {\text{ }}\dfrac{1}{2}$

Then, taking natural logarithm on both sides, we get
\[\ln \left( {{e^{\dfrac{{ - t}}{{RC}}}}} \right){\text{ }} = {\text{ }}\ln \left( {\dfrac{1}{2}} \right)\]
Further, we get
$\dfrac{{ - t}}{{RC}}{\text{ }} = {\text{ }}\ln \left( {\dfrac{1}{2}} \right)$
Then, we get
\[\dfrac{t}{{RC}}{\text{ }} = {\text{ }}\ln \left( 2 \right)\]
Thus, we get
$t{\text{ }} = {\text{ }}RC{\text{ }}\ln (2)$

Hence, the correct option is B.

Note: Students should be cautious while manipulating the equations. Students should be especially cautious while doing the logarithmic manipulation as the fractions sometimes make the manipulation very clumsy.An inductor opposes the changing current in it. In simple words, when the current increases in the inductor, the inductor induces a current such that the induced current decreases the in-flowing current.