Question

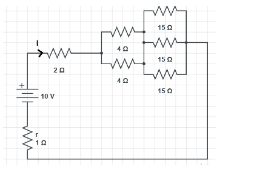
In the Circuit shown in figure, the current \[I\] has a value equal to

\[\begin{align}
  & A.IA \\
 & B.2A \\
 & C.4A \\
 & D.3.5A \\
\end{align}\]

Answer 1

Hint: When we see these types of circuit try to find out which resistor is connected in series and which is connected in parallel combination. This will simplify the circuit and we are able to calculate net resistance and therefore the required current. Net Resistance in series \[{{R}_{series}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+.....+{{R}_{n}}\] and Net Resistance and parallel \[\dfrac{1}{{{R}_{parallel}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}....\dfrac{1}{{{R}_{n}}}\].
Formula Used:
\[V=IR\]
This is known as Ohm’s Law. Where:
\[V=\]Potential Difference across the circuit
\[I=\] Electric current in the circuit
\[R=\]Resistance in the circuit
And we use,
Resistors connected in series, the net resistance:

\[{{R}_{series}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+.....+{{R}_{n}}\]

Resistors connected in parallel, the net resistance:

\[\dfrac{1}{{{R}_{parallel}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}....\dfrac{1}{{{R}_{n}}}\]

Complete step by step answer:
Here three \[15\Omega \] and two \[4\Omega \] resistors are connected in parallel.
For parallel the resultant resistance is:

\[\dfrac{1}{{{R}_{parallel}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}....\dfrac{1}{{{R}_{n}}}\]

And for \[n\] number of resistance connected in parallel

\[{{R}_{parallel}}=\dfrac{R}{n}\]

\[\begin{align}
  & {{R}^{'}}_{parallel}=\dfrac{15}{3} \\
 & {{R}^{'}}_{parallel}=5\Omega \\
\end{align}\]

\[\begin{align}
  & {{R}^{''}}_{parallel}=\dfrac{4}{2} \\
 & {{R}^{''}}_{parallel}=2\Omega \\
\end{align}\]

Now, \[R=2\Omega \], \[{{R}^{''}}_{parallel}=2\Omega \], \[{{R}^{'}}_{parallel}=5\Omega \] and internal resistance \[r\] are connected in series. We know that:

\[{{R}_{series}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+.....+{{R}_{n}}\]

\[\begin{align}
  & {{R}_{series}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+r \\
 & {{R}_{series}}=2\Omega +2\Omega +5\Omega +1\Omega \\
 & {{R}_{series}}=10\Omega \\
\end{align}\]

Also,
\[V=IR\]

\[\begin{align}
  & I=\dfrac{\varepsilon }{{{R}_{net}}} \\
 & I=\dfrac{10}{10} \\
 & I=1A \\
\end{align}\]
Hence, the correct answer is option A.

Additional Information:
Resistance: Resistance is the obstruction in the path of electric current. Or it opposes the current to flow in the circuit.

EMF: EMF or electromotive force, it is not a force. EMF of the cell is the amount of work done in moving the unit test charge from one point of circuit to other point (i.e. throughout the circuit).
Or the EMF is the potential difference between the electrodes of a cell in an open circuit (i.e. when no current is drawn from the cell).

Current: Current is defined as the rate of flow of electric charge through any cross section of the conductor. Current flows from positive to negative direction or opposite to the flow of electrons. It is a scalar quantity.

Internal Resistance: Resistance offered by the electrolyte inside the cell in flow of electric current is called internal resistance of the cell. It is denoted by \[r\].


Note: When resistors are connected in series, current is the same and potential difference is different along each resistor.
When resistors are connected in parallel, potential difference will be the same and current is different along each resistor.